Understanding Hypothesis Testing in Experiments

When Designing an Experiment and Analysing The Results, It Is Important to Consider Both Type I And Type II Errors. What Are the Various Issues That Arise in This Context, How Should the Research Approach These Problems, And Why Is It Important for Researchers to Consider These Issues?

INTRODUCTION

When experiments are being conducted, they are usually based on probabilities, meaning there is always an opportunity for making conclusions that are not correct. Due to this, there lacks a hypothesis test that is 100% accurate (Depoy & Gitlin, 2019). The process of utilizing information generated from a sample in order to determine if a hypothesis is valid or not, often requiring statistics dissertation help, is known as hypothesis testing (Luo, 2018)

For a significance test to be conducted, there has to be development of a null hypothesis (H0) also known as the original hypothesis and an alternative hypothesis (Ha), also known as the research hypothesis (List el., 2019). The null hypothesis (H0) represents no difference between parameters of a population of interest (Abdi, 2010), researchers usually gather evidence against this hypothesis (Luo, 2018). On the other hand, the alternative hypothesis (Ha) represents changed parameters of a population and researchers usually strive to gather evidence to support this hypothesis (McIntyre, 2013)

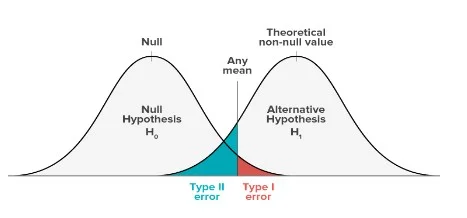
When performing a hypothesis test, there are two types of errors that present themselves: The type I error and type II error (List et al., 2019). There exists an inverse relationship in the risks presented by these two errors. These risks are determined by the power of the test and the significance level of the test. It is therefore crucial to find out which of the errors contains more series repercussions for the situation at hand before the risks are defined (Lee & Hotopf, 2012).

TYPE I AND TYPE II ERRORS

A type I error develops when the null hypothesis is true but it is not accepted. The possibility of creating a type I error is alpha (α). This is the significance level that is set for that hypothesis test (McIntyre, 2013).

For example, a 0.05 α signifies that the researcher is inclined to receive a chance of 5% that they are wrong when they reject the null hypothesis. In order to reduce the risk, the α value has to be lowered. However, the use of a lower value for α indicates that it will be unlikely to identify a true difference if it actually exists (List et al., 2019).

In the case of type II error, the null hypothesis is not true but it is accepted. Beta (β) is the probability of causing a type II error, which is dependent on the power of the test (Luo, 2018). The risk of committing the type II error can be reduced by ensuring that the test has enough power. For instance, making the sample size large big enough to identify a practical difference only when it truly exists (Depoy & Gitlin, 2019).

The odds of a null hypothesis being rejected if it is incorrect is equated to 1- β. This value signifies the power of the test (Luo, 2018).

Table 1. Representation of the Type I and Type II errors. Source:

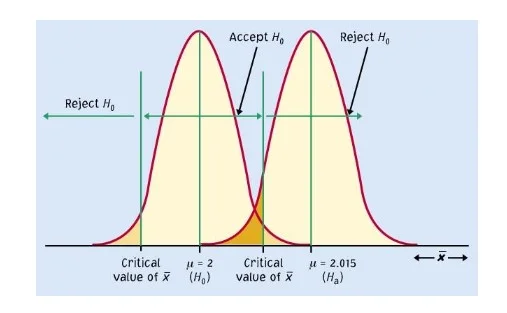
Image 1. Graphical representation of the Type I and Type II errors.

Arising Issues and the Approaches

There exists a mutually exclusive relationship between type I and type II errors. This means that reduction of the chances of occurrence of type I error leads to increased chances of occurrence of type II error and vice versa (Abdi, 2010). In addition to this, it is challenging to ascertain if either of the errors has been made since the actual parameters of the population of interest are unknown by the researcher (McIntyre, 2013).

The making of a type I error has been studied to have more adverse effects due to a significant outcome or relationship when none actually exists. Since other practitioners or researchers may act on that discovery, the research might want to safeguard against type I errors (Lee & Hotopf, 2012) Nonetheless, a type II error might also pose severe effects towards a professional practice if there is failure to acknowledge a positive result from a research. For instance, based on an accurate discovery, a productive and valuable intervention may be dismissed (Depoy & Gitlin, 2019)

The more there is comparison of statistics, the higher the likelihood of type I and type II occurrence (Justin & Po-Ling, 2020). In an experiment where there is a tremendously huge burden of statistics being compared, for instance neuroimaging analyses, it means that the type I and type II errors will occur more frequently than in other fields. In order to account for this issue, there should be implementation of statistical adjustments to correct for multiple comparisons (List et al., 2019). This can be achieved by correcting a statistical threshold depending on the number of comparisons being carried out. Some of the most frequently used methods of correction include: The Bonferroni Correction; the Sid`ak correction; correction for False Discovery Rate (FDR) and rectification of the Family-Wise Error Rate (FWER) (Abdi, 2010).

Inflation of the alpha level is a problem that occurs when the null hypothesis for rare events is rejected yet the bigger the test number, the easier it gets to detect rare events which are false alarms. To solve this issue, when undertaking multiple test, the alpha level needs to be adjusted. If the alpha level is made more rigid (i.e., smaller) few errors will be created, but it might be difficult to identify real effects (Justin & Po-Ling, 2020). To correct this, the Bonferroni correction is adopted and it comprises multiplication of each probability by total number of tests carried out (Abdi, 2010).

There exists a more powerful test that has a high likelihood of detecting an effect if any exists. This test was developed by Holm in 1979 and is known as the Holm Bonferroni method (Luo, 2018). In this method, the tests need to be carried out first to derive their probability values (p-values). The tests are then arranged from the one with the least probability value to the one with the greatest probability value. The Bonferroni correction is then used to assess the test that has the least p-value incorporating all tests. The second one is assessed with the Bonferroni correction incorporating all tests except one. This process carries on with the remaining tests until they are all done (Depoy & Gitlin, 2019).

When performing a family of tests (multiple tests), it highly likely that more than one type I errors will occur, this is what is referred to as the Family Wise Error (FWE) and the Bonferroni method is included (List et al., 2019). In a bid to limit the risks the occurrence of type I error in any of the statistical tests being carried out, it is necessary to correct for FEW (Depoy & Gitlin, 2019). Unfortunately, this correction is usually rigid, hence it increases the probability of occurrence of type II error (McIntyre, 2013). On the other hand, the FDR mainly aims at reducing the figure of false positives by controlling the data of Type I errors within all results that are significant (Banerjee et al., 2009).

it is not easy to choose between the FWE and the FDR, but the choice made is based on the type of software in use, because most of the software tools incorporate either of the two as an option that is default to check for multiple comparisons (Johnson & Gregory, 2019).

According to Lee & Hotopf, (2012), in any Literature, it is impossible to avoid the differences in results between studies. This, however, should not be viewed as a problem or even requiring any clarification beyond the issues due type I and type II errors. It is very normal and is expected for studies that have been very well conducted with similar methodologies and aims to detect false findings and miss the true ones in both of them. In such a case, it is expected to view the estimates of consequences of the studies produced to be classified around a single value that is of ‘best guess’.

However, in reality a research experiences studies whose sample sizes are not the same and methodologies are also different and in different settings. If the literature has a body that points in the same direction then the message brought out can be clear, but if there is a disagreement in the studies, then the researcher has to make sense out of it (McIntyre, 2013)

To avert the development of type II error then the significance level must be high (Justin & Po-Ling, 2020). On the other hand, reduction of the level of significance reduces the probability of a type I error occurring (Lee & Hotopf, 2012)

The Importance of Researchers to Consider These Issues

To demonstrate the importance of these issues, consider this real-life example:

A research on two drugs is been done to determine how effective they are against treatment of malaria. The null hypothesis in this case would be that the two drugs are equally effective (H0: μ1= μ2), whereas for the alternative hypothesis, the effectiveness of the drugs is not equal (H1): μ1≠ μ2). Therefore, a type I error would happen when there is rejection of the null hypothesis and a conclusion made that the two drugs are not the same when the truth Is that they are equal in effectiveness. The error made in this conclusion might be less severe since individuals with malaria will still benefit from an equal degree of effectiveness despite which drug is taken. However, in the case of a type II error being made, the null hypothesis is accepted instead of being rejected. The conclusion will be that the two drugs are the same in effectiveness when in truth they are different. The error made here will have very adverse impacts if the less potent drug will be released to the population and consumed instead of the drug that is more potent.

Another real-life example is: if a research for tuberculosis (TB) is being conducted then there are three instances that could occur. The first instance is that if TB truly exists and an early diagnosis is made, then it can be successfully cured which is the right thing to do. The second option is that if an early diagnosis for TB is made but not cured, then the patient might die, this is a case of type I error which has severe consequences. The third option is that if TB is not diagnosed but treatment is done, then the patient is not damaged physically, which is a case of type II error.

It is therefore crucial to put into consideration the type I and type II errors as they might have severe consequences after conclusions have been made (Banerjee et al., 2009).

CONCLUSION

A researcher is not able to ‘disprove’ or ‘prove’ anything simply by conducting statistical tests and hypothesis testing. What can be done, is rejecting or knocking down the null hypothesis and accepting the alternative hypothesis by default. If the researcher does not reject the null hypothesis, it is accepted by default.

It is very critical to put into consideration the risks of creating the type I and ii errors while conducting a hypothesis. If the occurrence of type I error causes impacts that are serious and costly than the impacts of making a type II error then a choice should be made based on the test power and the significance level that reflects the relative seriousness of those impacts.

REFERENCES

Abdi, H. (2010). Holm’s sequential Bonferroni procedure. Encyclopedia of research design, 1(8), 1-8.

Banerjee, A., Chitnis, U. B., Jadhav, S. L., Bhawalkar, J. S., & Chaudhury, S. (2009). Hypothesis testing, type I and type II errors. Industrial psychiatry journal, 18(2), 127.

DePoy, E., & Gitlin, L. N. (2019). Introduction to research E-book: Understanding and applying multiple strategies. Mosby.

Johnson, E. B., & Gregory, S. (2019). Huntington's disease: Brain imaging in Huntington's disease. In Progress in Molecular Biology and Translational Science (Vol. 165, pp. 321-369). Academic Press.

Justin Khim & Po-Ling Loh (2020): Permutation Tests for Infection Graphs, Journal of the American Statistical Association,/p>

Lee, W., & Hotopf, M. (2012). Critical appraisal: Reviewing scientific evidence and reading academic papers. In Core Psychiatry (pp. 131-142). WB Saunders.

List, J. A., Shaikh, A. M., & Xu, Y. (2019). Multiple hypothesis testing in experimental economics. Experimental Economics, 22(4), 773-793.

Luo, X. (2018, August). Theoretical Study on the Hypothesis Testing P Value. In 2018 2nd International Conference on Education Science and Economic Management (ICESEM 2018). Atlantis Press.

McIntyre, L. L. (2013). Parent training interventions to reduce challenging behavior in children with intellectual and developmental disabilities. In International Review of Research in Developmental Disabilities (Vol. 44, pp. 245-279). Academic Press.

Looking for further insights on Understanding Experiences and Enhancing Learning? Click here.