Exploring DCL Confidence Intervals

1. Introduction and Literature Review

1.1 Introduction

Dixon (2012) and Dixon and Bihan (2012) introduce the general Taylor model into the monetary economics. In the general Taylor model, there exists the cross-sectional distribution named as the Distribution of the Completed Lifetimes (DCL). Since the DCL is a new distribution, there is no method to investigate the confidence interval for it. The confidence interval of DCL is very important since the confidence interval can be applied to check whether the estimator of the DCL is rejected or not. In this paper, we introduce the numerical method-Fieller’s method to construct the confidence interval of the DCL. We also introduce the delta method to derive the confidence interval. In addition, the bootstrap Fieller’s method and bootstrap delta method are also introduced and applied to construct the confidence interval. Monte Carlo simulation is applied to compare the accuracy of those methods. Our purpose is that we want to find out whether those confidence intervals obtained from different methods are valid or not.

Literature Review

The confidence interval of the DCL and age distribution can be calculated by Fieller (1954)’s method and delta method. Tian and Dixon (2018) have derived the variance of the distribution of duration, age distribution and the DCL. In this paper, the variance formulas are applied in constructing the confidence interval of DCL since the variance of the duration and DCL are included in the formula of Fieller’s method and delta method. In Fieller’s method, the ratio distribution is transformed to a linear function. The confidence interval can be obtained by solving out the linear function. Fieller (1932) investigated and derived the general cumulative distribution formula for the ratio distribution. Both x and y followed the normal distribution and they were correlated with each other. The skulls of those ratio distributions were plotted. Fieller (1954) focused on the distribution of the ratio where x and y were independent with each other. Since DCL is a ratio distribution, it is worth to introduce the Fieller’s method to construct the confidence interval. With respect to the delta method, it is a robust method even when we do not know the distribution of the ratio variables. Alternatively, we can derive the probably density function of the DCL directly. Marsaglia (1965) derived the distribution that a normal variable is over another normal variable written as . Both x and y were random variables followed by the normal distribution; c and d were constant variables. Cedilnik et al. (2004) derived the probability density of the ratio variable w = x/y when x and y followed the bivariate normal distributions. Due to this property, the ratio distribution w had the same performance as the Cauchy distribution so that exist the first moment and the higher moment of it did not exist. They also focused on the shape of the density of the distribution w. They defined the shape estimator and investigated it under three conditions: (a) the sign of shape estimator was positive; (b) the sign of shape estimator was negative; (c) shape estimator was equal to zero. They gave the density function when x and y were perfectly correlated with each other (the correlation coefficient is equal to 1 or -1). In terms of the existence of the moment for the ratio distribution, see Cedilnik et al. (2006). However, it is hard to derive the density function of the DCL since the expression of the DCL is complicated. Therefore, we focus on the confidence interval rather than the density function of DCL. Comparing with the traditional numerical method, the bootstrap method is used widely to study the statistical inference. Efron (1979) introduced the bootstrap method, a powerful method to re-sample the original sample and evaluate the statistical inference. This method was applied by Efron (1981) in the survival analysis when censoring observations could exist. The bootstrapped data was applied to calculate the variance of Kaplan-Meier (KM) estimator. Those results were compared with the Greenwood formula which was the analytic variance formula of the KM estimator. Efron (1981) showed that the bootstrap variance of the KM estimator calculated from the bootstrapped data was close to the value of the Greenwood formula. Therefore, we also introduce bootstrap method to investigate the confidence interval of DCL.

Hwang (1995) introduced the bootstrap method into the ratio distribution. The bootstrap method can be applied to derive the confidence interval of the ratio distribution without any restrictions of the numerator and denominator. In other words, the numerator and denominator can follow any other distribution rather than the normal distributions. Both the parametric and non-parametric bootstrap method is applied to construct the confidence interval. In addition, the convergence ratio is evaluated between the Fieller’s method and the bootstrap method. Both methods provided the accurate convergence ratio. However, the bootstrap provided the second order correction for Fieller’s method. When the variables in the ratio formula do not follow the normal distributions which give a low converge ratio, the bootstrap method can be applied to improve it. There are some studies which focus on the comparison of the Fieller’s method with any other numerical methods. As Polsky et al. (1997) and Briggs et al. (1999) showed, the Fieller’s method and the parametric bootstrap method were suitable for constructing the confidence interval of the ratio distributions. Fan and Zhou (2007) suggested that the Fieller’s method, the standard bootstrap method and the bootstrap percentile method provided quite accurate confidence intervals when the numerator and denominator followed the different distributions. Depending on the simulation work of Wang and Zhao (2008), they suggested that the bootstrapped version of the Fieller’s method provided the more accurate confidence interval. Bebu et al. (2016) applied the Fieller’s method, the delta method and the bootstrap method to construct the confidence interval of the ratio variables. In Bebu et al. (2016)’s simulation studies, the Fieller’s method provided a more accurate result than the remaining methods. Also see Cox (1990) and Gardiner et al. (2001). Therefore, we are going to use those methods to investigate the confidence interval of the DCL and make the comparison among them.

The Properties of Age Distribution and DCL

Breslow and Crowley (1974) showed that the survival function Sˆi with i = 0,1,2,......,F followed the normal distribution, the vector V = (Sˆ0,Sˆ1,.....,SˆF ) a.s. follows the asymptotic multivariate normal distribution: V ∼ MN(E(V ),Σ). Where Σ is the variance-covariance matrix for the vector V , and the vector E(V ) is the mean value of each element in vector V. With respect to the age distribution, it can be written as ˆ . We define a new variable

which follows the asymptotic normal distribution

Now the µSˆ is E(Sˆ) and the is the variance of Sˆ. The age distribution is a ratio distribution ˆ . The distribution of the Sˆi and Sˆ follows the asymptotic multivariate normal distribution:

Where the µSˆi is the mean value of the Sˆi; µSˆ = µSˆ1 + µSˆ2 + ...... + µSˆF ; the variance of; the variance of

and k 6= j; σSˆi,Sˆ is the covariance of Sˆi and

). The variance and the covariance formula of the survival function are found from equation (1) and (2).

The survival function can be known as the Kaplan-Meier estimator (KM estimator). There exist the variance and the covariance of the KM estimator. The variance of the KM estimator was derived by Greenwood (1926). The general formula for the KM estimator can be written:

It is crucial to investigate the covariance amongst the survival functions. It is clear that the survival function Sˆi is correlated with Sˆj. Breslow and Crowley (1974) investigated the large sample properties of the hazard function and the survival function and they found that the off-diagonal variance covariance matrix of the hazard functions are all equal to zero while the diagonal terms are asymptotically equivalent with the formula derived by delta method. If the hazard hˆi with i = 1,2,......,F are collected by the vector hˆ, the joint distribution of the vector h follows the Gaussian distribution asymptotically. They also show that the vector of survival function V = (Sˆ0,......SˆF ) converge weakly to the Gaussian process. They derived the asymptotic covariance of the survival functions among different periods. Tsai et al. (1987) wrote a literature review to discuss the covariance properties of KM estimators. Tian and Dixon (2018) have applied the Taylor expansion method to derive the covariance of the KM estimators:

Define the estimator of DCL as ˆ . Where distribution of

duration can be defined as ˆadi = Sˆi−1hˆi. Since we know that the Sˆi−1hˆi =

Sˆi−1 − Sˆi. Therefore, Sˆi and the summation of the survival function Sˆ = follows the asymptotic normal distribution. It can be shown that Sˆi−1−Sˆi and Sˆ follow the multivariate normal distribution asymptotically:

In other words, the Cov(iSˆi−1hˆi,Sˆj) can be transformed to the covariance of Cov(iSˆi−1hˆi,Sˆ):

Cov(iSˆi−1hˆi,XSˆk) = i[Cov(Sˆi−1,XSˆk) − Cov(Sˆi,XSˆk)]

= i[XCov(Sˆi−1,Sˆk) −XCov(Sˆi,Sˆk)]

Note that) where Sˆ = (S0,S1,......SF ).

Using equation (2), we can calculate Cov(Sˆi,Sˆ).

The variance of DCL is derived by Tian and Dixon (2018) which can be written as:

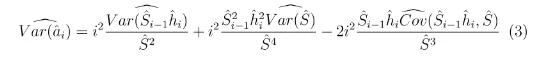
After holding those properties, Fieller’s method can be applied to construct the confidence interval.

Confidence Interval for the DCL

The Fieller’s Method

In this section, the confidence interval (CI) of DCL is given. Since age distribution is a special case of DCL, we just show the CI for DCL. The DCL can be estimated as ˆ . The DCL can be written as ai =

. It is exact to the ratio of distribution. To simply the expression of the ai, assume the numerator iSi−1hi = xi, and the denominator .

Therefore, the DCL can be expressed as ai = xi/y at period i.

In the DCL formula, the denominator is always above zero. Normally, the mean value of the summation of survival function should be a positive value. If the denominator is close to zero, the CI for xi/y is not accurate. There are several methods can be applied to estimate the confidence interval.

Fieller (1940, 1954) gave a method to derive the confidence interval of the ratio variables. It required that ˆxi and ˆy followed the bivariate normal distribution asymptotically. They are not independent with each other:

ai = xi/y can be modified as:

xi = aiy

As Fieller had explained, the bivariate distribution function v = f(xi,y) with a given value ai existed in the linear function xi = aiy. It can be rewritten as:

xi − aiy = 0

Replace the xi and y by the estimator ˆxi and ˆy , separately. Now there exists the new relationship:

xˆi − aiyˆ a.s.∼ N(0,V ar(xˆi − aiyˆ))

Thus a new statistic can be written as:

Where H(ai) follows the student-t distribution with the degree of freedom d. If ˆxi and ˆy are approximate as asymptotic normal rather than exact normal, the degree of freedom d can be assumed as infinite. There exist the relationships:

P[H(ai) < t1−α/2(d)] = 1 − α/2

Where α is the type I error; t1−α/2(d) is the critical value found in the student-t table; d is the degree of freedom. We also have:

P[L(ai) < 0] = 1 − α/2

The function L(ai) can be defined as:

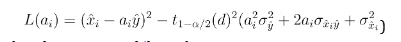
Open the bracket, equation(5) can be written as:

L(ai) = F1 − 2F2ai + F3a2i

As can be seen from the formula (6), the function L(ai) is a quadratic form of the DCL ai. Where ; . To find out the confidence interval of the DCL ai, we can define the notations (F2 + B1/2)/F3. As Buonaccorsi (1954) showed, the confidence interval of ai can be defined as [B1,B2] when both the F2 and the B are not less than zero. If B is not less than zero while the F2 > 0, the confidence interval is (−∞,B2] and [B1,∞).If both B and F2 are less than zero, the confidence interval of ai is (−∞,∞). The confidence interval of DCL ai can be written as: (7) By replacing ˆxi = iSˆi−1hˆi and ˆ into F1, F2 and F3, we can get: F1 = (iSˆi−1hˆi)2 − t1−α/2(d)2i2V ar(Sˆi−1hˆi)

F2 = iSˆi−1hˆi(XSˆk) − t1−α/2(d)2iCov(Sˆi−1hˆi,XSˆk)

F3 = (XSˆk)2 − t1−α/2(d)2V ar(XSˆk)

In the statistic area, researchers prefer the bounded confidence interval to the unbounded confidence interval. The denominators of the age distribution aˆAi and DCL aˆi are the summation of the survival function. We can use to compare with t1−α/2(d)2 and find out whether Sˆ = 0 or not. It is equivalent to check whether F2 is positive or negative. In terms of this, the confidence interval of the ratio variables is unbounded. See Guiard (1989) for the unbounded confidence interval of the ratio variables.

Delta Method

Delta method can be also known as the Taylor expansion method. Assume the survival function Sˆi converges to the mean value Si. The survival function Sˆi follows the asymptotic normal distribution:

Where Ni is the sample size at i − th period. is the Greenwood formula.

Depending on the Taylor expansion:

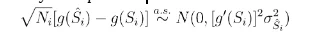
g0(Si) can be replaced by g0(Sˆi) since [is an estimator of V ar[g(Sˆi)] where). It can be derived by Taylor expansion:

g(Sˆi) = g(Si) + g0(Si)(Sˆi − Si) + Op((Sˆi − Si)2)

Delta method is also available for the ratio distribution ˆai = xˆi/yˆ. The first-order Taylor expansion of ˆai = xˆi/yˆ approximated at the mean value E(xˆi) = xi and E(yˆ) = y is:

In terms of the variance:

This variance formula can be also rewritten as:

The 1-α/2-th point-wise CI of ai obtained from delta method can be defined as:

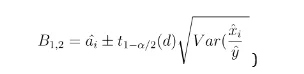
Where) and this can be calculated from the equation (3).

Even the ˆxi/yˆ may not follow the normal distribution, it is worth to investigate the CI derived by delta method since delta method is robust. Depending on the estimator ˆai, the σxi and σy are replaced by σxˆi and σyˆ in equation (8). In addition, xi and y are replaced by ˆxi and ˆy directly. In other words, the xi ≈ xˆi and y ≈ yˆ and this could also be applied to derive the Greenwood formula. If the denominator is close to zero, the delta method is not available.

Bootstrap

The bootstrap method is a resampling method given by Efron (1979). The Pairs bootstrap method for the survival analysis is introduced by Efron

Pairs Bootstrap and Censored Data

Following Efron (1981)’s paper, it can be assumed that there exist the variable Xn which is independent and identically distributed follows the the unknown distribution D with n=1,2,......N. The parameter θ(D) can be any estimators such as OLS, maximum likelihood, KM estimator or DCL. The estimator can be written as θˆ = θ(Dˆ). The bootstrap standard deviation of θ can be defined as σ∗ and obtained from the bootstrap sample. With respect to the non-parametric bootstrap, the details of the bootstrap process are: step 1. assign the equivalent probability 1/N to each Xn. Then, the bootstrap sample) can be drawn from the distribution of Dˆ independently. More specially, the bootstrap sample) is a new set with the independent N observations which are re-sampled from the original sample X = (X1,X2,......,XN) with can be any number ranging from 1 to N. Therefore, some observations Xn may exist more than once and some of them are not included in the bootstrap sample. After that, the bootstrap empirical distribution D∗ can be generated. Step 2. Depending on this bootstrap sample X∗ and distribution D∗, we can get∗ the bootstrap estimator thetaˆ. To repeat the bootstrap process (step 1 and 2) for B times, there exists the number of B estimators.

The bootstrap standard deviation can be calculated by the formula:

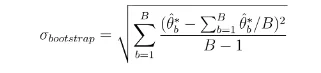
The non-parametric bootstrap method can be available for the pairs observations. Therefore, the non-parametric bootstrap method of step 1 and 2 can be replaced by the process as below. Assume there exist the pairs observations (X,Y ) = ((X1,Y1),(X2,Y2),......,(XN,YN)). In other words, a unique Xn corresponds to a unique Yn. To bootstrap those pairs observations, it can be directly resampled from (X,Y ). More specially, the pair (Xn,Yn) from (X,Y ) is assigned by the equivalent probability 1/N and re-sampled to obtain the (X∗,Y ∗). The bootstrap sample can be written as ( )). Those () can be equal to (Xj,Yj) in the original pairs (X,Y ); j can be any number ranging from 1 to N. It can be seen that some pairs may exist more than once while some of them may not exist in the bootstrap sample. This method is known as the Pairs bootstrap method. The bootstrap empirical distribution D∗ can be generated by the bootstrap pairs sample (X∗,Y ∗). The KM estimators and the DCL can be calculated from the bootstrapped sample. The formula is given in the next section. With respect to the survival observation, the maximum length of the events is assumed to last F period. Nk means the total events survived at the k − th period with k = 0,1,......,F. Define the Tn as the n-th events survival time while n = 1,2,......N. The observed lifetime can be defined as: tn = min(Tn,Cn) and ωn = I(Tn ≤ Cn) n = 1,2,......N. Where the Cn means that whether the n−th sample is right censored or not at the right bound point, ωn is the censored coefficient. If the observation n is uncensored, ωn is equal to 1. Otherwise, it is equal to zero.

Tn ≤ Cn, tn = Tn (uncensored) ωn = 1

Otherwise,

Cn ≤ Tn, tn = Cn (right censored) ωn = 0

Now the bootstrap method can be linked to the survival data. When the n-th observation is uncensored, the coefficient of ωn is equal to 1 while it is equal to 0. It could be assumed that the survival time follows the rule t1 < t2 < ...... < tN. Therefore, the survival data can be rewritten as (t1,ω1),(t2,ω2),......,(tN,ωN). They are organized from the smallest value t1 to the biggest value tN. If the censored observations are not considered, all the parameters of the ωn = 1 and the tn = Tn, the sample ((T1,1),(T2,1),......,(TN,1)) can be thought as (T1,T2,......,TN). The bootstrap sample can be written as. After that, repeat this process for B times, the bootstrap sample can be applied to calculate the KM estimator. In terms of the censored observations existing in the data, some ωn may not equal to 1. To bootstrap (tn,ωn): step 1. the bootstrap sample can be written as (). It means that the bootstrap sample is drawn independently from the original sample. It assigns the 1/N probability for each pair (tn,ωn); step 2. the bootstrap sample (t∗,ω∗) can be applied to calculate KM and DCL estimators; step 3. repeat the step 1 and 2 for B times to get the Bootstrap version survival and DCL estimators; step 4. Those estimators can be applied to calculate the bootstrap standard deviation or variance. The restriction is that it requires the observation (tn,ωn) to be the i.i.d observations from the unknown distribution D.

Bootstrap the Variance of the DCL

In this section, the bootstrap method is applied to derive the variance of DCL and compared with the benchmark value and the analytic results derived by Tian and Dixon (2018). Since the survival time is not exactly the same for each Monte Carlo simulation and the bootstrap, the survival data can be reorganized and divided into special F-categories. In other words, the data can be assigned into some intervals such as (0,r1],(r1,r2],....(rk−1,rk],.....(rF−1,rF ]. The value for them is depending on the data set. Followed by that, we can be generated as a new dataset. Define the Nk to be the number of the observations in the k-th intervals; k = 1,2,......,F. More specially, we can count the number of the observations Dk located in (rk−1,rk]. If all the observations are uncensored, we also have the relationships . Depending on this rule, we can also define and and apply them to calculate the bootstrap Kaplan-Meier estimator and the Nelson-Aalen estimator. The bootstrap Kaplan-Meier estimator can be written as:

is the number of agents or people survive at k-th interval (period). ”∗” means this data is collected from the bootstrap sample. Since the bootstrap sample is re-allocated and divided into F categories. Dk∗ is the number of agents or people die at the k-th period. There exist the relationships Nk∗ −Nk∗+1 under the uncensored situation. The bootstrap NA estimator can be written as:

The is the bootstrap NA estimator which is also known as the cumulative hazard function. With respect to the bootstrap version of the marginal hazard rate hˆ∗i , it can be written as:

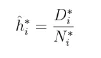
Since we have both the bootstrap KM and NA estimators, they can be applied to calculate the distribution of duration, the age distributions and the DCL. The distribution of duration can be written as:

It can be explained as the proportion of observations survive for (i − 1) periods and die at the i-th period. Therefore, the bootstrap version of the distribution of the duration can be written as:

The variance of the ˆadi is derived by Tian and Dixon (2018), it can be written as:

While for the bootstrap variance of the adi∗, it can be written as:

Where ˆ is the distribution of duration in the b-th bootstrap re-sample process. B is the absolute number of the bootstrap re-sample processes. The age distribution can be written as:

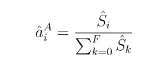
The bootstrap age distribution can be written as:

It means that the bootstrap variance of the DCL a∗i can be calculated from each bootstrap sample for b = 1,2,......,B. B is the total number of the bootstrap re-sample times. Define, the variance formula of the KM estimator in bootstrapped version can be written as:

We have the bootstrap covariance formula:

The Bootstrapped CI of the Ratio Variables

The bootstrapped Fieller’s method means that we use bootstrap sample to calculate the critical value and construct the confidence interval. The bootstrapped Fieller’s method was applied by Hwang (1995); Wang and Zhao (2008). The bootstrapped estimators of the and hˆ∗i are applied. Define the ˆ and ˆ . Following the Fieller’s theorem, the bootstrap formula of the H(ai)∗ can be written as:

H(ai)∗ can be known as the bootstrap version of the H(ai). The bootstrapped Fieller’s method is applied to find out the α/2-th and (1-α/2)-th smallest value of H(ai)∗ in the bootstrap sample. Assume the original sample has been bootstrapped B times. The H(ai)α/2∗ and H(ai)1−α/2∗ is the α/2-th and (1-α/2)-th smallest value of the bootstrap statistic H(ai)∗. ”α/2∗” means the α/2’s smallest value in the bootstrap sample. It should be mention that there exist the relationships t1−α/2(d) = −tα/2(d). In other words, the ratio statistic satisfied H(ai)1−α/2 = −H(ai)α/2. However, it may not exactly follow the symmetric rule when the sample size is not big enough. At this point, H(ai)1−α/2∗ is replaced by−H(ai)α/2∗ when the upper bound of the confidence interval of ai is calculated. The convergence ratio can be expressed as:

P[−H(ai) < H(ai)α/2∗] = α/2 (25)

Alternatively, it can be expressed as:

P[H(ai) > H(ai)1−α/2∗] = α/2 (26)

In addition, the bootstrapped confidence interval can be constructed. The two sided bootstrapped confidence intervals from Fieller’s method can be written as:

In the equation (27) ,the critical value of the t statistic t1−α/2(d) is replaced by the bootstrap value H(ai)1−α/2∗. In terms of the equation (28), the tα/2(d) is replaced by the bootstrap value H(ai)α/2∗. It should be mention that H(ai)α/2∗ applied to calculate the upper bound due to the bootstrap properties. The bootstrapped-t value may not be the symmetric case. In other words, it is exactly different from the symmetric -t distribution. Therefore, both the H(ai)α/2∗ and H(ai)1−α/2∗ must be applied to construct the confidence intervals for the ratio ai. Another point is that they all have the square value in the andso that (H(ai)1−α/2∗)2 replaced by (H(ai)α/2∗)2 directly.

With respect to the delta method, the bootstrap-t confidence interval is also available. The ratio statistic derived from the delta method can be treated as:

) is the variance of DCL which can be calculated from equation (3). is the lower bound;is the upper bound; Since the bootstrap-t

critical value may not be the exactly symmetric relationship, the and need to be used in the equation (30) and (31), respectively.

Monte Carlo and Pairs Bootstrap Simulation

The Pairs Bootstrap of the Variance

In this part, we use the Monte Carlo simulation and pairs bootstrap to compare the analytic results of the variance, the bootstrapped variance and the benchmark value. The benchmark value of variance means the variance is calculated from the Monte Carlo simulation directly. In other words, the benchmark value of the variance of DCL can be treated as the true value of the variance. Following Kiviet and Phillips (2014)’s method, the true value of the variances for DCL can be defined as:

Where the ˆ means the estimator of the distribution of duration from the m-th simulation sample with m = 1,2,......,M. To generate the survival data, we follow the steps as below: Step 1: The observations are assumed to follow the exponential distribution functions. The probability density function of the n-th observation can be written as:

p(Tn) = 2exp(−2Tn) (35)

The probability density function of the n-th censored time can be written as:

p(Cn) = 0.5exp(−0.5Cn) (36)

The survival function for each rk-th period can be defined as:

p(Cn > rk) = exp(−0.5rk) p(Tn > rk) = exp(−2rk) (37)

Where n = 1,2,.....,N and k = 1,2,......,F. N is the total number of the observations in the sample and F is the maximum length of the period. Both the censored and uncensored problems are considered at this point. If the uncensored observations are there, the survival time of observations Tk is applied to draw the sample directly. On the other hand, the Tk is compared with the Ck due to the existing of the censored assumptions. In addition, those observations are assigned into five categories: (0,0.1], (0.1,0.2], (0.2,0.3], (0.3,0.5] and (0.5,∞). This can be known as case 1. In case 2, the observation are allocated in another five categories: (0,0.2], (0.2,0.4], (0.4,0.6], (0.6,0.8] and (0.8,∞). Therefore, the variance of the duration and the DCL can be calculated by the asymptotic formulas. Step 2: The pairs bootstrap is applied to resample the original sample. Step 3: Repeat the step 2 by B = 1000 times. After bootstrap B = 1000 times, the bootstrapped variance can be calculated directly from the bootstrap sample. Step 4: Repeat step1, step 2 and step 3 for M = 5000 times. The true value of the variance can be calculated directly by applying the 5000 original sample. It means that there are 5000 original samples. Each sample is bootstrapped by 1000 times. Therefore, there are 5000 bootstrap variances of the duration and the DCL. The mean value of the bootstrap variances is calculated and compared with the true value and the analytic formula. Table 1 is the result for the variance of the duration. The sample size is chosen to be N = 50. The variances calculated from the analytic formula and the bootstrap variance of the distribution of duration is close to the benchmark true value. With respect to the table 2, it is the empirical results of variance of the DCL. The asymptotic approximation variance provides an accurate result which is close to the benchmark variance. The bootstrap variance still shows a good performance and provided an accurate result. Table 3 and 4 are the empirical results for the case 2. It can be seen that the approximation variance calculated from the formula and the bootstrap method are nearly the same as the true variance. In addition, both the bootstrap method and the asymptotic expansion method provide the accurate results of the variance. Table 5 to 8 show the empirical results of the variance when censored observations could be in existence. Depending on the empirical results, both the bootstrap variance and the variance calculated from the analytic formula are close to the benchmark variance. Therefore, both the bootstrap method and the delta method can be applied to calculate the variance of the Table 1: The Variance of the Duration of Uncensored Result for Case 1. All the Results Are Multiplied by 103 and the Sample Size N=50 True Value

Note:) is the benchmark value calculated from formula (34); E[Var(adi )] is the variance of duration calculated from formula (14); E[Vard(adi∗)] is the bootstrapped variance of duration calculated from formula (15).

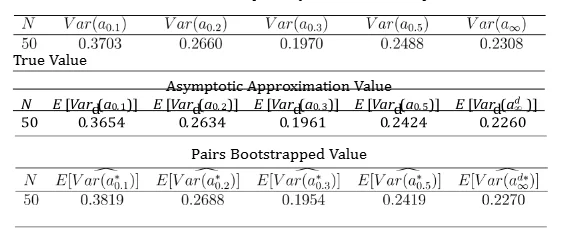
Note: Var(ai) is the benchmark value calculated from formula ( is the variance of duration calculated from formula (3); )] is the bootstrapped variance of duration calculated from formula (20).

Note:) is the benchmark value calculated from formula (34); E[Var(adi )] is the variance of duration calculated from formula (14); E[Vard(adi∗)] is the bootstrapped variance of duration calculated from formula (15).

Note: Var(ai) is the benchmark value calculated from formula ( is the variance of duration calculated from formula (3); E[Var(a∗i )] is the bootstrapped variance of duration calculated from formula (20).

distribution of duration and DCL.

Note:) is the benchmark value calculated from the formula (34); E[Var(adi )] is the variance of duration calculated from the formula (14); E[Vard(adi∗)] is the bootstrapped variance of duration calculated from formula (15).

Note: Var(ai) is the benchmark value calculated from formula ( is the variance of duration calculated from formula (3); and E[Var(a∗i )] is the bootstrapped variance of duration calculated from formula (20).

Note:) is the benchmark value calculated from formula (34); E[Var(adi )] is the variance of duration calculated from formula (14); E[Vard(adi∗)] is the bootstrapped variance of duration calculated from formula (15).

Note: Var(ai) is the benchmark value calculated from formula ( is the variance of duration calculated from formula (3); E[Var(a∗i )] is the bootstrapped variance of duration calculated from formula (20).

The Confidence Interval of DCL

In this section, the CI of the Fieller’s method, Delta method, bootstrapped Fieller’s method, bootstrapped delta method and percentile bootstrap CI have been investigated. The simulation process is the same as that of section 5.1: Step 1: In this section, we focus on the CI rather than the variance. Both the survival time Tk and censored time Ck followed the exponential distribution introduced in section 5.1. The sample size is N = 25, 50, 200 and 400. The Fieller’s statistic H(ai) and the delta statistic H(ai)delta are calculated for each Monte Carlo simulation. The significant level α is chosen to be 10 percent. Step 2: The pairs bootstrap is applied to get the bootstrapped value from the Fieller’s formula H(ai)∗ and delta method. The bootstrapped version of the confidence of the Fieller’s method and delta method can be calculated by the bootstrapped sample. Step 3: Repeat the step 2 by B = 1000 times. Therefore, there exists 1000 H(ai)∗. Reorganize those 1000 value of H(ai)∗ start from the smallest to the largest value and find out the +1 and (1 +1 smallest value of H(ai)∗. Since the significant level α is 10 percent therefore, α/2-th smallest value of H(ai)∗ is applied to be the lower bound and the 1−α/2-th smallest value of H(ai)∗ is applied to the upper bound of the distribution of DCL. This 1 − α/2-th smallest value of H(ai)∗ can be known as H(ai)1−α/2∗. The α/2-th smallest value of H(ai)∗ can be known as H(ai)α/2∗. In terms of the delta method, the bootstrapped version of the critical value and are calculated. Step 4: Repeat step 1-3 by M = 5000 times when sample size N = 25,50; choose M = 1000 when the sample size N = 200 and 400. Each Monte Carlo simulation followed by the 1000 bootstrap simulations. After that, the simulation result can be applied to calculate the average value of the lower bound and upper bound to increase the power. The benchmark value of the CI can be calculated depending on the percentile method, The Monte Carlo results of ai can be a re-order from the smallest to the largest. Then α/2-th and 1 − α/2-th smallest values are chosen to be the lower bound and the upper bound separately.

Table 9, 10, 11 and 12 list the different confidence intervals under the uncensored and censored conditions, respectively. Table 9 shows the CI of the DCL when N = 25. The first column is the true CI which is simulated from the Monte Carlo method. There are five methods to calculate the confidence

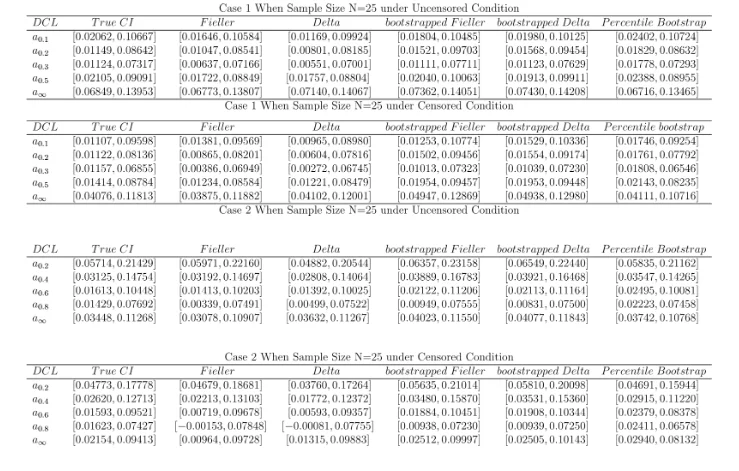
interval. Those confidence intervals are compared with the true confidence intervals. Fieller’s method always provides the accurate results for the upper bound of the confidence interval while lower bound exist some biases. In the first three periods, Fieller’s method is superior to the delta method while both methods perform well in the last two periods. In terms of the bootstrap method, they give the significant bias results. It should be mention that there exists the negative value of the lower bound in case 2 with the censored situation. The negative value is due to the extremely small sample size in that category. Kalbfleisch and Prentice (2002) provided a log-log transformation method to derive the confidence interval of the KM estimator. Since the DCL is between 0 and 1, the log-log transferred confidence interval provided by Kalbfleisch and Prentice (2002) can be considered for DCL when the negative value of the confidence interval exists. In the table 10, the Fieller’s method provides a quite accurate confidence interval over the five categories when the sample size is 50. The delta method does not work very well compared with the Fieller’s method in the first three periods while both of them give the quite accurate results in the last two periods. In terms of the bootstrapped version, the confidence intervals provided by bootstrapped Fieller’s and delta methods are not accurate in small sample sizes. Table 11 and 12 show the results when the sample size is 200 and 400. In the large sample sizes, all the five methods provide very similar results.

Conclusion

In this paper, we used the Filler’s method, the delta method, bootstrapped Fieller’s method, bootstrapped delta method and the bootstrap percentile method to derive the CI for the DCL. In addition, the pairs bootstrap method is applied to derive the variances of the distribution of the duration and the DCL. Since the DCL is a new inference in the survival analysis, the variance derived by Tian and Dixon (2018) is compared with the bootstrap variance. The simulation studies show that the pairs bootstrap can provide the accurate results for variances of the duration distribution and the DCL. The empirical results show the both the bootstrap variance and the analytic variance of the distribution of duration and DCL are close to the benchmark value. In terms of the confidence interval of the DCL, the empirical results show that the CI of DCL derived by Fieller’s method is superior to the remaining method when the sample size is below 50. The bootstrapped Fieller’s method, the bootstrapped delta method and the bootstrap percentile method do not work well when the sample size is below that of 50. However, all the five methods provide the accurate confidence intervals when the sample size is above 200. In addition to this, the bootstrapped variance of duration and DCL perform well even when the sample size is 50.

Reference

Bebu, I., Luta, G., Mathew, T., Kennedy, P. A., and Agan, B. K. (2016). Parametric cost-effectiveness inference with skewed data. Computational Statistics and Data Analysis, 94:210–220.

Breslow, N. and Crowley, J. (1974). A large sample study of the life table and product limit estimates under random censorship. Annals of Statistics, 2:437–453.

Briggs, A. H., Mooney, C. Z., and Wonderling, D. E. (1999). Constructing confidence intervals for cost-effectiveness ratios: an evaluation of parametric and non-parametric techniques using monte carlo simulation. Statistics in Medicine, 18:3245–3262.

Buonaccorsi, J. P. (1954). Fieller’s theorem. Encyclopedia of Environmetrics, pages 773–775.

Cedilnik, A., Koˇsmelj, K., and Blejec, A. (2004). The distribution of the ratio of jointly normal variables. Metodoloˇski zvezki, 1(1):99–108.

Cedilnik, A., Koˇsmelj, K., and Blejec, A. (2006). Ratio of two random variables: A note on the existence of its moments. Metodoloˇski zvezki, 3(1):1–7.

Cox, C. (1990). Fieller theorem, the likelihood and the delta method. Biometrics, 46(3):709–718.

Dixon, H. (2012). A unified framework for using micro-data to compare dynamic time-dependent price-setting models. BE Journal of Macroeconomics (Contributions), 12:1–43.

Dixon, H. and Bihan, H. L. (2012). Generalised taylor and generalised calvo price and wage setting: Micro-evidence with macro implications. Economic Journal, 122:532–554.

Efron, B. (1979). Bootstrap methods: Another look at the jackknife. The Annals of Statistics, 7(1):1–26.

Efron, B. (1981). Censored data and the bootstrap. Journal of the American Statistical Association, 76(374):312–319.

Fan, M. and Zhou, X. (2007). A simulation study to compare methods for constructing confidence intervals for the incremental cost-effectiveness ratio. Statistics in Medicine, 7:57–77.

Fieller, E. C. (1932). The distribution of the index in a normal bivariate population. Biometrika, 24:175–185.

Guiard, V. (1989). Some remarks on the estimation of the ratio of the expectation values of a two-dimensional normal random variable (correction of the theorem of milliken). Biometika, 31(6):681–697.

Kiviet, J. F. and Phillips, G. D. A. (2014). Improved variance estimation of maximum likelihood estimators in stable first-order dynamic regression models. Computational Statistics and Data Analysis, 76:424–448.

Marsaglia, G. (1965). Ratios of normal variables and ratios of sums of uniform variables. Journal of the American Statistical Association, 60(309):193– 204.

Polsky, D., Glick, H. A., Willke, R., and Schulman, K. (1997). Confidence intervals for cost-effectiveness ratios a comparison of four methods. Health Economics, 6(3):243–252.

Tian, M. and Dixon, H. (2018). The confidence interval of cross-sectional distribution of completed lifetimes and the pairs bootstrap. Working Paper.

Tsai, W. Y., Jewell, N. P., and Wang, M. (1987). A note on the product limit estimator under right censoring and left truncation. Biometrika, 74(4):883–886.

Wang, H. and Zhao, H. (2008). A study on confidence intervals for incremental cost-effectiveness ratios. Biometrical Journal, 50:505–514.