Calculations
Task 1: (5 marks)
Identify the numbers and buttons you would press on your calculator. Showing the steps in reaching your answer (2 decimal places), explain in words how you would calculate the following:

-
2.96= Step 1= Pressing the first numeral 2 on the calculator.
Step 2= Identification and pressing of the Decimal Point (.).
Step 3= Pressing of the second numeral 9.
Step 4= Identification Square value of the input measure through the button of XY and activation of the same on the calculator.
Step 5= Pressing of the Enter button.Answer=594.823321.
Revised Answer with value up to 2 decimal points=594.82.
-
532 = Step 1= Pressing the required numeral value buttons to enter the value of 32.
Step 2= Selecting the entire value in the scientific calculator.
Step3= Finding and pressing the Inversion function key in the form of INVx button so as to multiplicative inversion of the value of x which is 32 in this calculation.
Step 4= Selecting the yx format from the inverse value based options.
Step 5= Entering the inverse value numerator of 5 in the appropriate place. The outcome should resemble the inverse value of the entered numerical.
Step 6= Initiating the calculation through pressing the =/Answer key/button.
Answer=2
-
1/(1+0.02)4= Step 1= Entering the value of the denominator in the scientific calculator in the form of 1.
Step 2= Entering the division command through identification and pressing of the backslash right indent key in the calculator in the form of (/).
Step 3= Entering the value of the numerator in the format of (1+0.02) at the appropriate segment of the entire calculation.
Step 4= Identification and activation of the to the power superscript command key on the calculator in the format of xy so as to enter the square root value necessary to the entire value of the numerator.
Step 4= Putting in the required value of 4 at the appropriate position. Step 5= Activation of the Answer key. Answer= 0.92384542602.
-
500x5-2 = Step 1= Entering the initial value of the number which has to be multiplied in the form of 500.
Step 2= Pressing of the multiplication key (x) on the scientific calculator.
Step 3= Entering the value of the multiplicative numerical in the form of 5.
Step 4= Identification of the root to the power superscript key on the scientific calculator in the format of xy to put in the negative square root value to the equation.
Step 5= Entering the negative square root value in the form of (-2) at the appropriate segment.
Step 6= Activation of the Answer key on the calculator. Answer=20.
-
23.15+√50/0.9875-3.25
= Step 1= Determination of the development of solution to the denominator first.
Step 2= Entering the numerals of the initial section of the denominator in the form of 23.05.
Step 3= Addition of the next section of the denominator through identification and pressing of the square root (√) key on the calculator and adding the rest of the numerals as √50.
Step 4= Completion of the addition through pressing of Answer key.
Step 5= The outcome is 30.2210678119.
Step 6= Next, performing the subtraction task outlined in the numerator through entering the numeral values and then subtracting them from each other.
Step 7= The value obtained from the subtraction of the numerals of the Numerator is -2.2625.
Step 8= Finally, dividing the Denominator by the Numerator is performed in the calculator.
Answer= -13.3573780384.

Task 2
Mariana phones her mum in New York. Phone calls to New York are charged at the rate of £2.20 for a 5-minute call.
-
How much would a 7-minute call to New York cost?
-
Mariana’s call costs £5.28. How long (in minutes) was her call? The charge attributed to Mariana has been determined as £5.28. Thus, it could be calculated that, £2.20 is the cost when the call time is 5 minutes. £1 is the cost when the call time is 5/2.20 minutes. £5.28 is the cost when the call time is =5/2.20x5.28 =5x100 ______x528 220 =12 minutes. Answer
Ans: A 5 minute call is charged at the rate of £2.20 A 1 minute call is charged at the rate of £2.20 /5 A 7 minute call is charged at the rate of £2.20 /5x7 = £3.08. Answer
Task 3
4 people can paint a fence in 3 hours. How long will it take 6 people to paint the same fence (Assume everyone works at the same rate). You must show all your workings.
Answer: 4 individuals could paint the fence within 3 hours. 1 individual could paint the same fence within 3x4 hours 6 individuals could paint the same fence in= 3x4/6 hours = 2 hours. Answer
b) 12 men take 5 days to build a road 200m long. How many days will 20 men take to build a similar road which is 400m long? Explain your answer in details.
Answer: 12 men have to work for 5 days to construct the road with length of 200 mts. 1 man has to work for 5x12 days to construct the road with length of 200 mts. 20 men have to work for 5x12/20 days to construct the road with length of 200 mts. 20 men have to work for 5x12/20 x 1/200 days to construct the road with length of 1 mts. 20 men have to work for 5x12/20 x 1/200 x 400 days to construct the road with length of 400 mts= 60/20 x 400/200=6 days. The answer is 6 days. c) Super Paint is mixed by using yellow and blue in the ratio 7:2
i) How much yellow and how much blue must be used to make 72 litres of the super paint?
Answer: The ratio of the mixture of yellow and blue colours in the super paint is that of 7:2. The required volume is that of 72 litres.
Let it be supposed that the quantity of both yellow and blue colours of the super paint within the 72 litres would x respectively. Thus, x would be the common denominator for both of the quantities of the colours. Thus, 7x+2x= 72 9x= 72 x=8 Thus, the quantity of yellow would be 7x8=56 litres. The quantity of blue would be 8x2=16 litres. ii) How much blue is used if 35 litres of yellow is used? Let it be supposed that the overall quantity of the combined liquid is x. Thus, as per the stated condition, 7/5=x/35 or 5x=35x7 or x=49 Thus, 49 litres of yellow paint has been utilised. Answer.
Task 4
The future value of an annuity is given by FV = PV x (1 + R)n Find the future value (FV) if the present value of £ 9,500 is invested for 6 years at an annual interest rate of 2.35%. Give your answer correct to the nearest £.
Answer: As per the stated conditions, the Present Value (PV) is £ 9,500. As per the stated conditions, the period of investment is 6 years. As per the stated conditions, annual interest rate is 2.35%. Thus, as per the stated formula, FV = PV x (1 + R)n or FV= 9,500 x (1+2.35)6 or FV= 1413.41222139x 9,500 or FV=13427416.1032 or FV= £13427417 (correct nearest to the £).
b) A garage offers car service which costs £90 plus VAT at 20%.
i) Calculate the amount of VAT charged is 20%.
Answer: As per the stated conditions, charged rate of VAT is 20%. The car service cost is £90 in total. Logically, the Value Added Tax would cost about 20% of the car service cost. Thus, 20% of the car service cost amounts to the following, 20x90/100= 18. Thus, the answer is £18.
ii) What is the total cost of the service?
The total cost of the service is Car Cost (£90)+ Value Added Tax (£18) =£108. Mr Jones receives an electricity bill for £56.84. The bill includes a quarterly charge of £10.40 and the cost per unit is 6.85 pence. Calculate to the nearest whole number, the number of units he has used. Answer: As per the stated conditions, the quarterly charge count is £10.40. Since the complete electricity bill for the entire year is £56.84. As per the stated conditions, the combined quarterly charge is £ (10.40x3)= £31.2. Furthermore, the amount which remains after deduction of the combined quarterly charge is=£(56.84-31.2)= £25.64= 25.64=2342.32 pence. As per the stated conditions, the individual unit cost is 6.85 pence. The individual numbers of unit could be determined as the following, 2342.32 /6.85= 341.944525547 units=342 units (nearest whole number). Answer is 342 units.

Task 5: (2 marks)
You decide to play the National Lottery, where you have to choose 6 different numbers between 1 to 59 inclusive.
Explain in words how you would calculate the possible combinations of winning the jackpot (i.e. obtaining all six numbers). Show all the steps in your calculation.
(You should not use the formula in the calculator)
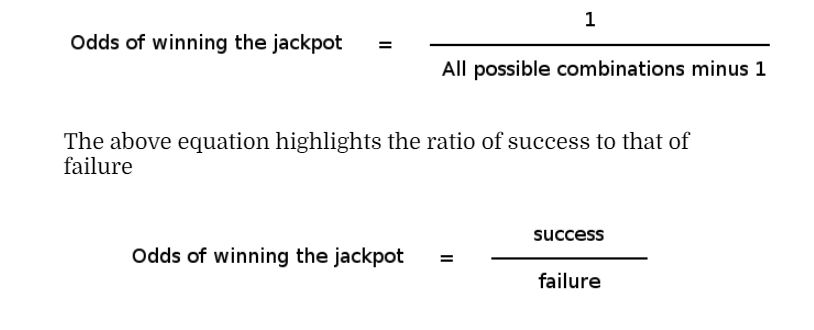
Ans: Since the odds of playing the lottery is primarily designed for the loss of the player in the majority of the draws, the focus of the player has to be on winning at the comparatively less frequency to win the jackpot. However, this involves Availability Bias which could prompt a player to ignore the Confirmation Bias. To this effect, the theoretical approach involves the evaluation of odds of winning the jackpot in the National Lottery in the following manner:
Mathematically, counting the odd and even numbers play a crucial role in your chances of winning the From a mathematical perspective, the odd and even numbers have to be counting accurately so that the chances of winning the National Lottery could be increased. The following table outlines the complete extent of odd-even numerical patterns along with the corresponding probability of theirs:
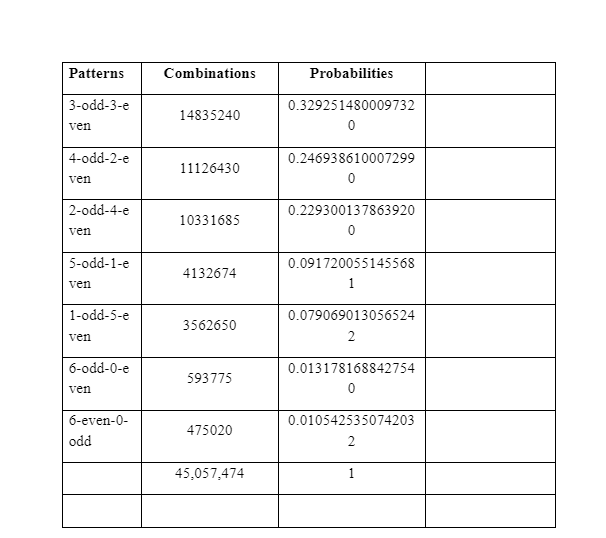
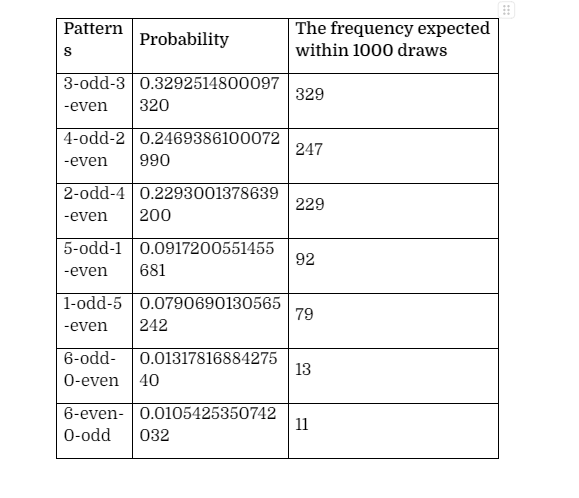
For instance, the outcome of the UK Lottery, if it is to be known in advance, in, hypothetically, 1000 draws, then the utilisation of the following formulation of all of the expected frequencies is utilised: Expected frequency (3-odd-3-even) = 0.3292514800097320 x 1000 draws In this context, it could be observed that for every 3-odd-3-even combination, the frequency to be expected would be 329.2514800097320 or 329 (as the nearest whole number). If it is required to forecast accurately, the outcomes of every pattern of odd-even numbers, the ensuing patterns would always be on the 3odd-3 even sequence.
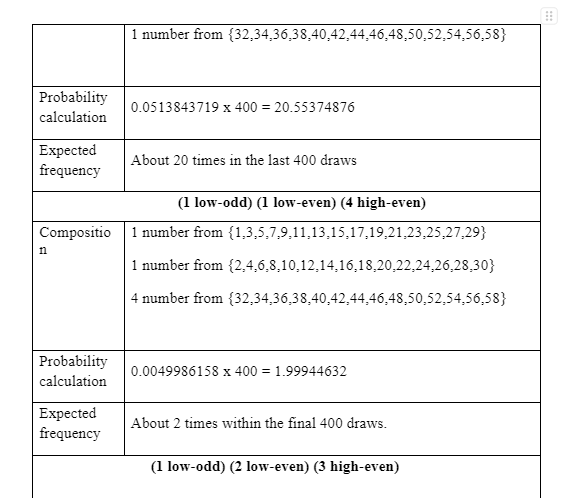
However, this sequence of odd and even draws could not properly delineate the UK Lottery structure since, at a considerable depth within the finite structure of the National Lottery system, various layers of advanced patterns exist which are the primary determinants of the success regarding the lottery outcomes. The application of Applied Mathematics is significant in terms of discovery of such advanced patterns. For instance, 1,2,3,4,5,6 could belong to the pattern of 3-odd-3-even numbers. This format of sequential combination is considered to be the best pattern in this context and is primarily derived from the One low-odd, One low-even and Four high-even pattern. The following 4 sets could delineate these patterns better: Low-odd=(1,3,5,7,9,11,13,15,17,19,21,23,25,27,29) Low-even=(2,4,6,8,10,12,14,16,18,20,22,24,26,28,30)
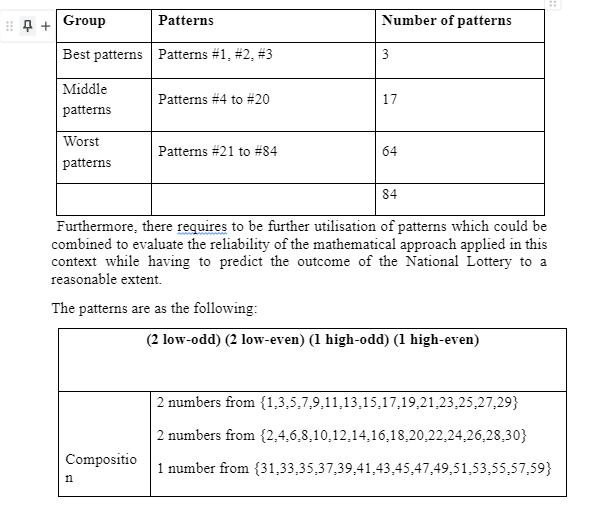
High-odd=(31,33,35,37,39,41,43,45,47,49,51,53,55,57,59) High-even = (32,34,36,38,40,42,44,46,48,50,52,54,56,58) The examples of differential combinations involving the above demonstrated pattern are as the following: 5-18-32-38-42-54 19-28-36-40-52-58 Thus, the probability of the above demonstrated pattern is 0.0049986158. The UK Lotto is identified to have a total of 84 patterns and only 3 of those could be understood to be suited for the purpose of effective forecast. These could be divided into 3 specific groups:



Task 8: (6 marks)
Jill owns a fabric store and earns £2.50 for each metre of cotton and £3.50 for each metre of silk she sells. Jill sold 45 metres of silk last year. She earned a total of £780 last year selling cotton and silk. Write an equation that can be used to determine the amount of cotton sold last year. Answer: £780-(£3.50x45)/ £2.50 How much cotton did Jill sell last year? Answer: As per the stated conditions, the sale of 45 metres of silk has occurred within the previous year. The cost price of per metre of silk is £ 3.50. Thus, the complete earnings from sales of 45 metres of silk has been the following: 45x3.50=£157.5. As per the stated conditions, the complete earning has been £780 during the previous year. Thus, Jill had sold the following amount of cotton: £780-(£157.5)/ £2.50=717 metres of cotton have been sold during the previous year. Jill claims that she can earn more money this year by selling only 1/3 of the amount of cotton she sold last year and 3 times the amount of silk sold last year. Explain if her claim is correct. Answer: As per the stated conditions, sale of 1/3 cotton would entail the following for Jill: 717/3=239 metres (since it has been already determined that Jill had sold 717 metres of cotton during the previous year). As per the provided information, the existing cost of each metre of cotton is £2.50. Thus, 239 metres of cotton sold would be fetching the following amount of revenue for Jill: 239x £2.50= £597.5. Furthermore, as per the stated information previously, the amount of silk sold during the previous year has been 45 metres and the cost price of each metre of silk has been £3.50. Thus, with the sales of silk purported to increase up to 3 times, the amount of silk which would be sold would be: 45 x 3=90 metres. The sales price of 90 metres would be =90x£3.50=£315. The combined earning would be=£315+£597.5=£912.5 During the previous year, the combined income of Jill had been £780. Thus, Jill would be able to earn=£912.5-£780=£132.5 greater.


Apples are 𝒙 pence per kg. Oranges are 𝒚 pence per kg. 5 kg of apples and 30 kg of oranges cost £41.40 5 kg of apples and 27 kg of oranges cost £37.80 Write down two equations connecting 𝒙 and 𝒚 Ans: As per the provided information, the combined cost price of 5 kg of apples and 30 kg of oranges is £41.40. On the other hand, the combined cost price of 5 kg of apples and 27 kg of oranges is £37.80. Thus, the cost price for 5 kg of apples at the price of 𝒙 pence per kg is =£5x Thus, the cost price of 30 kg of oranges at the price of 𝒚 pence per kg is=£30y By the previously stated conditions, the combined cost price for 5 kg of apples and 30 kg of oranges is=£41.40
Dig deeper into By the end of the session the student will develop with our selection of articles.
Task 10: (6 marks)
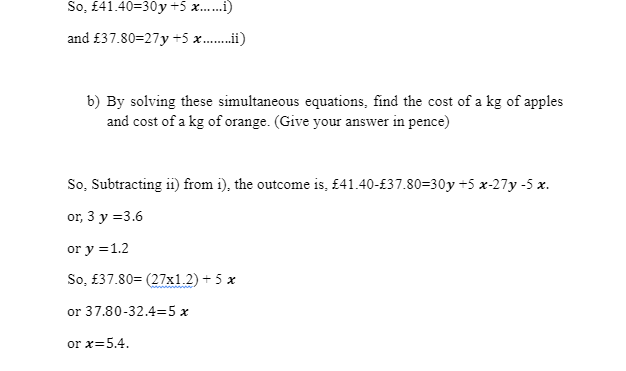

- 24/7 Customer Support
- 100% Customer Satisfaction
- No Privacy Violation
- Quick Services
- Subject Experts



