Fashion Goods and Market Demand

Introduction

In the recent years, most of the people are involved with the fashion industry either as the customers in purchasing the products or as the producers or manufacturing for managing the product life cycle. The variety of fashion goods is becoming larger where the accessories, jewellery, perfumes, clothes, cars, home and many other products can be considered as fashionable goods. It is difficult for the decision makers to identify the fashionable goods as a particular product is a fashion good from a consumer point of view, but it may be considered as ordinary product for others. For example, buying a car for the middle class of a community is an ordinary good, but buying a car for a wealthy and well-off-minded people is a fashionable good. because of such complexity, scheduling of selling fashion items or production plan of these items is very important. Fashion is one of the most visible media of change. The fashion industry forms larger social and cultural phenomenon known as the “fashion system,” a concept that embraces not only the business of fashion but also the art of fashion, and not only production but also consumption. The peculiar nature of fashion industry can be characterized in terms of its volatility, velocity, variety, complexity and dynamism. The following graph shows that the demand for different markets is not constant between different periods of time and it is subject to numerous variables. For example, climate change in different seasons, inflation rates, and technological advances are some of the reasons why they can reasonably change market demand. Moreover, the inflation rate and income level of different classes of society, which plays an important role in the purchasing power of the people, and it can change the market for the sales of fashion goods. For example, when a country's sweat fluctuates unevenly due to war or internal changes in political structure, the purchasing power of the people of society is diminished, and the demand for fashionable goods naturally diminishes. Latin American countries and some countries like Syria are the examples of widespread inflation. On the other hand, the cultural structure of a country can also affects the consumption of fashionable goods. Asian countries are one of the main destinations for the sale of fashion goods in the world. For example, Saudi Arabia is the largest cosmetics importer in the world. Therefore, the presentation of a planning method for the sale of manufactured goods can lead to the ordering and sale of these goods internally and even abroad, which naturally reduces the import of these goods from countries such as China and, consequently, increases the domestic economic prosperity of a country in Will follow. A brief overview on fancy goods timing models shows that the timing of fashion goods has not been addressed by considering multiple retailers and retailers at different time periods when unlimited demand is considered. Therefore, the purpose of this study is to exclusively discuss the effects of possible market demand on the timing of the sale of fashion goods.

Literature Review

A supply chain involves all the stages (chain members), whether directly or indirectly, in fulfilling a customer's request. In a regular supply chain, raw materials are shipped from suppliers to factories. Then, the products produced in the factories are being transferred to middle warehouses and distribution depots, from which they also go to retailers and ultimately to the end customers or consumers. Therefore, a commodity is transferred through various stages of the chain to reach the consumer. In some of these stages, the goods are stored and shipped in some other places, where, a regular supply chain includes suppliers, warehouses of raw materials, production centres, distributors, retailers and final customers. The fundamental problem in fashion industries is that the time it takes to source materials, convert them into products and transfer them into the market place which is invariably longer than the time the customer is prepared to wait. Contemporary fashion industry is very global and dynamic. The importance of time as a competitive weapon has been recognized for some time. The ability to be able to meet the demands of customers for ever-shorter delivery times and to ensure that supply can be synchronized to meet the peaks and troughs of demand was analyzed by Christopher et al. (2004); Barnes and Lea-Greenwood (2006); Doeringer and Crean (2006); Stone (2008), Sull and Turconi (2008); Nagurney and Yu (2011); Runfola and Guercini (2013). Er study a variety of literature including academic articles, industry and case studies. We review (Jia and Hu, 2011) article ,The paper discusses the combined problem of pricing and ordering for a perishable product supply chain with one supplier and one retailer in a finite horizon. The lifetime of the product is two periods and demand in each period is random and price-sensitive. In each period, the supplier determines first a wholesale price and then the retailer decides an order quantity and retail prices. We show that, the optimal pricing strategy for the non-fresh product depends only on its inventory, and the optimal pricing strategy and the optimal order quantity for the fresh product depend only on the wholesale price and they have a constant relation. Moreover, the game between the retailer and the supplier for finite horizon is equivalent to a one period game with only one order. Thus, the optimal policies are identical at each period. For the additive and multiplicative demands, we further obtain equations to compute the optimal strategies. All above results are extended into the infinite horizon case and longer lifetime products. Finally, a numerical analysis can be discussed further (Jia, andHu, 2011) This paper considers a supply chain game with a buyer and a seller through pricing and ordering models with partial lost sales. We evaluate the optimal solutions for the buyer and the seller and provide insights into both the deterministic and stochastic demand models. We also propose search algorithms to obtain the global optimum when convexity and concavity conditions are not satisfied (Cia, et al., 2011) Continue your journey with our comprehensive guide to Fashion Goods and Market Demand.

In this paper, they determine the order quantity and the prices for a perishable product with a multiple period lifetime. Demands for products of different ages depends on the prices of mutually “substitutable” products. The problem for a product with lifetime of two periods is first analysed and the stochastic dynamic programming model is developed. For a product with lifetime of longer than two periods, a heuristic based on the optimal solution for a single period problem is proposed for a multiple period problem (Chew et al., 2014). Organizing the flow of returning goods in supply chain system is studied by chung et al, in 2011. There is deterioration of the negative impacts of the production on environment in the recent decades. Many articles are written about reverse logistic and recycling concept for getting closer to our problem. We try to review article which study reverse logistic about deteriorating items. For example, in this study, green product designs and remanufacturing efforts are investigated when we develop an integrated production inventory model with short life-cycles. A numerical example is provided by them to illustrate the theory. they have shown that new technology evolution, remanufacturing ratios and system’s holding costs are critical factors affecting decision making in a green supply chain inventory control system. (Hsueh, 2011) investigated, inventory control policies in a manufacturing/remanufacturing system during the product life cycle, which consists of four phases: introduction, growth, maturity, and decline. Both demand rate and return rate of products are random variables with normal distribution; the mean of the distribution varies according to the time in the product life cycle. Closed-form formulas of optimal production lot size, reorder point, and safety stock in each phase of the product life cycle are derived. A numerical example is presented with sensitivity analysis. The result shows that different inventory control policies should be adopted in different phases of the product life cycle. The proposed model by Weeet al, 2011 considers that the vendor managed inventory strategy and conducts a life cycle cost and benefit analysis for green electronic products. In their study, the mathematical analytical approach is used to solve the proposed model. The results show that selling price, deteriorating rate, holding cost, product return rate, and remanufactured quality have a significant effect on the model. Their study can provide managerial insights into improving the design of a green-supply chain Studies about supply chain system illustrated, these systems from perspective of flow of goods divided into three groups. Take a deeper dive into Childhood Supracondylar Fracture Analysis with our additional resources.

Forward supply chain, reverse supply chain, closed loop supply chain

Forward supply chain

It is the classic type and is the series of activities which can be done to flow raw material from supplier to producer and final production from producer to consumer, regarding to teymori 1388 the purpose in forward supply chain is to increase service levels and reducing the total cost.

Reverse supply chain

In recent decades regarding to shorten of goods life cycle and technology improvement, global warming and environmental pollution. Most of enterprises and companies pay huge attention to exploitation of resources and environmental protection. Therefore they try to reducing environmental concern by recycling, reproducing , repairing and reselling production (Chun-Jen Chung; Hui-Ming Wee, 2011) (Wee; Lee; Jonas; Wang, 2011) The profitability of remanufacturing depends on the quantity and quality of product returns and on the demand for remanufactured products. The quantity and quality of product returns can be influenced by varying quality-dependent acquisition prices, i.e., by using product acquisition management (Guider et al., 2003) In this paper, a closed-loop logistics system with manufacturing and remanufacturing cycle is analysed using three optimization methods. They are: (i) sequential optimization, (ii) centralized optimization without benefit sharing, and (iii) centralized optimization with benefit sharing. Four key effects are investigated in this study: (i) recycling in supply chain, (ii) deterioration, (iii) collaboration effect between manufacturer and retailers using three optimization methods, and (iv) price sensitive demand (Yang et al., 2013). According to the American Reverse Logistics Executive Council, reverse logistics is defined as “The process of planning, implementing, and controlling the efficient, cost effective flow of raw materials, in-process inventory, finished goods and related information from the point of consumption to the point of origin for the purpose of recapturing value or proper disposal” (Rogers and Tibben-Lembke, 1998). Indeed, reverse logistics, in general forms, start from end users (first customers) where used products are collected from customers (return products) and then attempts to manage EOL products through different decisions are undertaken including recycling (to have more raw materials or raw parts), remanufacturing (to resale them to second markets or if possible to first customers), repairing (to sell in the second markets through repairing), and finally, disposing of some used parts.( Govindan, et al., 2014)

closed-loop supply chain

A closed-loop supply chain (CLSC) network consists of both forward and reverse supply chains. In this paper, a CLSC network is investigated which includes multiple plants, collection centres, demand markets, and products (Amin and Zhang, 2013) Supply chain management (SCM) has received a lot of attentions. There are two types of supply chains: forward and reverse supply chains. The forward supply chain (FSC) contains of series of activities which result in the conversion of raw materials to finish products. Managers try to improve forward supply chain performances in areas such as demand management, procurement, and order fulfilment (Cooper, Lambert, and Pagh, 1997) (Abdallah, Farhat, Diabat, and Kennedy, 2012). Reverse supply chain (RSC) is defined as the activities of the collection and recovery of product returns in SCM (Melo, Nickel, and Saldanha-da-Gama, 2009 ). Nowadays closed-loop supply chain management known as effective, efficient and cost effective strategy among factories , it seems many researchers try to illustrate new scope of using this in their studies like (Amin, and Zhang, 2013) who work on article which developed facility location model for closed-loop supply chain network under uncertain demand and return, or (Chen,J-M,chang,2013) they work on Dynamic pricing for new and remanufactured products in a closed-loop supply chain (Winkler, 2011). Working on sustainable supply chain is considering closed-loop type. As we mention above, inventory management in organization play key role, because beside its effect on servicing consumer it can increase the total cost of organization too. This issue is important for companies which deal with deteriorating items in their production system. Recently regarding to improvement in technology and competitive markets and though consumers the quantity of deteriorating items increases (Li, et al., 2013) Despite of the situation of market finding suitable inventory strategy seems critical for companies.

Technological or fashion goods

Today, the attention of many scholars and researchers has focused on the issue of fashion merchandise or outdated goods. With the growth of fashion industry over the past few years, it has a significant share of the economy of the countries. Fashion markets are synonymous with rapid change and, as a result, commercial success or failure is largely determined by the organization’s flexibility and responsiveness. Responsiveness is characterized by short time‐to‐market, the ability to scale up (or down) quickly and the rapid incorporation of consumer preferences into the design process. Christopher, (2004) argued in their paper that, conventional organizational structures and forecast‐driven supply chains are not adequate to meet the challenges of volatile and turbulent demand which typify fashion markets. Instead, the requirement is for the creation of an agile organization embedded within an agile supply chain. According to Abecassis-Moedas, (2006), factors such as changing the trend of the fashion industry, the shorter life cycle of products associated with this industry, the intense competition for low-cost labor markets, the unprecedented growth of the emerging market, triggered Significant changes have been made in the traditional models of this industry. In their article, they analyzed the relations within the factory, such as the relations between producers and suppliers, as well as relations between producers and retailers, which are actually low members analyzing hand-drawn chains and doing research in the apparel industry, which is in fact a buy-oriented industry surgical described as a key success factor in this industry. Subsequently, with the strategy of design integration and retailing, they achieved a more flexible design process that increased the level of product performance.

Fashion goods supply chain

Many researchers work on fashion goods supply chain, in 2013 Jayaranthne present empirically based classification for clothing supply networks. They show diversity in network types that has not previously been shown. The comparison of networks of established brand retailers and value players provides empirical evidence of differences not reported previously. The findings enrich both the theoretical and empirical bases for sector‐specific supply network studies. Burn (2008) the paper presents the results of a research project focused on supply chain (SC) strategy in the fashion/apparel industry ongoing at Politecnico di Milano, aiming at assessing the relevance of Supply Chain Management (SCM) approach in a context, i.e. fashion, where operations and manufacturing seem to be considered as ancillary to marketing and communications activities. In this field sen, 2011 studied apparel supply chain risks. An attempt is made to study the ASC and identify the related risks in general and they provided a platform to identify the risks for an apparel supply chain in particular. Christopher (2004) argued that, conventional organizational structures and forecast‐driven supply chains are not adequate to meet the challenges of volatile and turbulent demand which typify fashion markets. Instead, the requirement is for the creation of an agile organization embedded within an agile supply chain. Anna Nagurney, (2011) studied sustainable fashion supply chain management under oligopolistic competition and brand differentiation. Li et al., in 2012, provided a comprehensive introduction about the deteriorating items inventory management research status, the paper reviewed the recent studies in relevant fields. Compared with the extant reviews (Raafat 1991; Goyal, 2001), this paper reviewed the recent studies from a different perspective. First, this paper proposes some key factors which should be considered in the deteriorating inventory studies; then, from the perspective of study scope. The current literatures distinguished into two categories: the studies based on an enterprise and those based on supply chain. Chris and cheng, (2012) studied The impact of environmental management systems on financial performance in fashion and textiles industries, they investigate that The production of fashion and textiles related products often requires high levels of energy and water consumption, and emits large quantities of pollutants to the environment. Therefore, the adoption of environmental management systems (EMSs) is important and could have a significant impact on these firms' operational performance. They try to study presents empirical evidence on the performance impact of EMS adoption in the fashion and textiles related industries (FTIs). Although EMSs have emerged as a passport to business in the FTIs, their actual impacts on firms' financial performance have not been explored. We reveal that, the adoption of ISO 14000, the most popular EMS, improves manufacturers' profitability in the FTIs over a three-year period as measured by return-on-assets (ROA). Based on their sample, they found that, profitability improvement started during the implementation stage and continued at least one year after the firm obtained ISO 14000 certification. We also find that profitability improvement is mainly due to improvement in cost efficiency, measured by return-on-sales (ROS). Specifically, certified firms improved up to 2.9% in ROA and 3.3% in ROS over the three-year period since they implemented ISO 14000. They concluded that there is a positive impact of EMS adoption on firms' financial performance in the FTIs. Federico caniato, (2014) developed a comprehensive framework to investigate the integration of the NPD process and international retail in the fashion industry with a contingency approach. In particular, the internationalization of retail is analysed by considering the influence of foreign countries’ characteristics on NPD. To achieve this goal, thirteen exploratory case studies of Italian fashion companies were performed. The cases allow the identification of the framework variables as well as the analysis of the relationships among those variables. Finally, the study shows that three main archetypes of behaviours are identified. Laura Macchion (2015) contributed to extend knowledge in the field of production and supply network strategy in the fashion industry. Analysing the supply network strategy literature, the paper investigated production and supply network configuration that fashion-industry firms implement to remain competitive in a global context. Statistical analysed on survey data from 132 Italian fashion companies highlight the existence of three different clusters of companies that have identified alternative ways to organise their production and supply networks that are aligned with their specific competitive priorities (e.g., critical success factors). The study characterises the three different clusters of production and supply strategies of fashion companies and provides useful interpretation of differences among clusters. Erfeng Zhou (2014) studied a two period pricing model for new fashion style launching strategy and the Results of their study showed that a fashion firm׳s optimal launching strategy is mainly determined by the production cost and the consumer׳s mental book value. In detail, (i) when the consumer׳s mental book value and/or the production cost are relatively high, N-Strategy is the firm׳s optimal choice; (ii) when the consumer׳s mental book value is low and the production cost is high, S-Strategy is the best strategy; and (iii) when both the consumer׳s mental book value and the production cost are relatively low, the D-Strategy dominates the other two.

Other article which we reviewed are mostly Previous research has focused on responding quickly to customer needs (Castelli,2010) (Bruce,2004) (Zhang et al., 2014) And Also, the coordination of the supply chain of fashion goods (Xio and Jin, 2011) (Casteli, 2010) We reviewed the article of Marzieh Mehrjoo et al., 2014 they study Impact of Product Variety on Supply Chain in Fast Fashion Apparel Industry, regarding to their study Contemporary customers change their product preferences rapidly and are inclined to purchase only what they need or want. In response, the companies need to increase their product variety to improve market share and remain globally competitive. Considering above issue in their study the focus of the proposed model is on the interaction between physical processes, information flows and managerial policies of the apparel supply chain in order to create the dynamics of the variables of interest such as product variety, inventory, backlogs, costs and profit. Many author works on cultural aspect and the influence of these issues in fashion industry (Erica P.das neves, 2015) (motagna, 2015) (Mario Joao Bravo Lima Delgado, 2015). (Yong Yu; Tsan-Ming Choi andChi-Leung Hui, (2011) they proposed a seasonal discrete grey forecasting model for fashion retailing. In their paper, they present a new seasonal discrete grey forecasting model based on cycle truncation accumulation with amendable items to improve sales forecasting accuracy. forecasting model is to overcome two important problems: seasonality and limited data. Although there are several works suitable with one of them, there is no previous research effort that overcome both problems in the context of grey models. The proposed algorithms are validated using real POS data of three fashion retailers selling high-ended, medium and basic fashion items. They found that the proposed model is practical for fashion retail sales forecasting with short historical data and outperforms other state-of-art forecasting techniques. Raffaele lannone et al, (2015) developed a Causal Loop Diagram for the definition of the cause and effect relationships between the several variables which define the system under exam. Being time a crucial variable in this field, in fact, dynamic complexity arises due to interaction of agents over time and evolving situations. Their work highlighted and analysed all the conflicting requirements that must be accurately evaluated and balanced in order to effectively manage the complex network of retailers and to help the decision-making process behind the purchasing, delivery and replenishment step. Considering the study of Young He (2010), the global markets of today offer more selling opportunities to the deteriorating items’ manufacturers, but also pose new challenges in production and inventory planning. From a production management standpoint, opportunities to exploit the difference in the timing of the selling season between geographically dispersed markets for deteriorating items are important to improving a firm’s profitability. Young He also examined the above issue with an insightful production-inventory model of a deteriorating items manufacturer selling goods to multiple-markets with different selling seasons. He also provided a solution procedure to find the optimal replenishment schedule for raw materials and the optimal production plan for finished products. A numerical example was then used to illustrate the model and the solution procedure. Finally, sensitivity analysis of the optimal solution with respect to major parameters was carried out. According to Kun Chen (2014), an analytic decision-making framework for multi-channel evaluation proposed. They first developed an analytic network, based on the inputs of managers and literature, to depict the interrelationships between decision criteria. Multi-Criteria Decision-Making methods are then adapted to determine the weight of each evaluation criterion and to rank the practicality of alternative marketing channels. The model is tested with Cisco China. Sensitivity analysis is conducted in order to understand the impact of criteria uncertainties on channel rankings and the robustness of the proposed model. The management at Cisco found the model to be transparent, logical, practical, and it provided a valid and reliable guide for evaluating channel alternatives. Zhang (2012) studied a multiple-market price discrimination problem with different markets’ demand elasticity and supply constraints, whereas the market shares a common capacity. They identify the problem as a continuous nonlinear knapsack problem and propose an efficient algorithm for solving the optimal solution after exploring the structural properties of the studied problem. Sensitivity analysis is done for better understanding the behaviour of the problem, and numerical results are provided to show the performance of the proposed method.

Liu Yang (2014) established a flexible capacity strategy model with multiple market periods under demand uncertainty and investment constraints. In the model, a firm makes its capacity decision under a financial budget constraint at the beginning of the planning horizon which embraces n market periods. In each market period, the firm goes through three decision-making stages: the safety production stage, the additional production stage and the optimal sales stage. they formulate the problem and obtain the optimal capacity, the optimal safety production, the optimal additional production and the optimal sales of each market period under different situations. They find that, there are two thresholds for the unit capacity cost. When the capacity cost is very low, the optimal capacity is determined by its financial budget; when the capacity cost is very high, the firm keeps its optimal capacity at its safety production level; and when the cost is in between of the two thresholds, the optimal capacity is determined by the capacity cost, the number of market periods and the unit cost of additional production. Furthermore, they explore the endogenous safety production level. They verify the conditions under which the firm has different optimal safety production levels. Finally, they prove that the firm can benefit from the investment only when the designed planning horizon is longer than a threshold. Moreover, they also derive the formulae for the above three thresholds. Seyed Mohsen Mousavi, (2014) Optimised multi-item multi-period inventory control system with discounted cash flow and inflation: Two calibrated meta-heuristic algorithms, a mixed binary integer mathematical programming model is developed in this paper for ordering items in multi-item multi-period inventory control systems, in which unit and incremental quantity discounts as well as interest and inflation factors are considered. Another article which we reviewed is Chung-Yuan Dye (2012) and they considered the amount invested in preservation technology and the replenishment schedule as decision variables. They provide a simple algorithm to figure out the optimal solution in their study and they investigated the change of the optimal solution and the total profit per unit time from the sensitivity analysis. Taylor (2001) revealed the study which examines three channel policies that are used in declining price environments: Price protection (P) is a mechanism under which the manufacturer pays the retailer a credit applying to the retailer's unsold inventory when the wholesale price drops during the life cycle; midlife returns (M) allow the retailer to return units partway through the life cycle at some rebate; and end-of-life returns (E) allow the retailer to return unsold units at the end of the life cycle. Further studies which we consider in our research is Ferguson (2006) indicating that, false failure returns are products that are returned by consumers to retailers with no functional or cosmetic defect. The cost of a false failure return includes the processing actions of testing, refurbishing (if necessary), repackaging, the loss in value during the time the product spends in the reverse supply chain (a time that can exceed several months for many firms), and the loss in revenue because the product is sold at a discounted price. This cost is significant and is incurred primarily by the manufacturer. Reducing false failure returns, however, requires effort primarily from the retailer, for example informing consumers about the exact product that best fits their needs. We address the problem of reducing false failure returns via supply chain coordination methods. Specifically, we propose a target rebate contract that pays the retailer a specific dollar amount per each unit of false failure returns below a target. This target rebate provides an incentive to the retailer to increase her effort, thus decreasing the number of false failures and (potentially) increasing net sales. We show that this contract is Pareto improving in the majority of cases. Our results also indicate that the profit improvement to both parties, and the supply chain, is substantial.

Research Methodology

In this section, the research method will be displayed as the flowchart (Fig. 3-1) As it is clear in this flowchart, the mathematical model, with the input information like the amount of market demand, retailer capacity, sales profits, as well as transport costs from the producer to the retailer, from the retailer to the market, Sellers and returns to the manufacturer. Further the mathematical model can find best (nearest) retailer and can achieved through retailers to the best market (a market that has more demand and less transportation cost). If the number of products received by each retailer is sold during the market period, there will be no need to transfer it to the upcoming period. Otherwise, the surplus of products will be auctioned at a later time between retailers and, if not sold during this period (regarding to fashion goods situation which explain before), this additional amount of the products will be fined, deducted from the total price of the product and return to producer. We want to find the best distribution of productions to retailers and then to distribute these goods in the target markets in such a way that the highest profitability of the commodity will be earn by the producer.

Flow chart diagram

Developing a Model for Planning

We consider demand for products in different planning periods is not constant and is estimated from the triangular distribution function. The reason for considering the triangular distribution function is the ability to consider three optimistic, pessimistic, and most probable values for each demand that these market conditions (bestseller, moderate, and low-selling) are applicable.

In summary, the features of the model presented in this study can be summarized as follows:

• Consider the fashion goods • Consider the potential demand for sales planning • Taking inventory of products • Consider the return of the product

Assumptions

1. The demand for various time periods is not constant and follows the triangular distribution function. 2. Each market has a specific rate of demand. 3. If the goods are not sold at a later period, they will be auctioned at a lower price if they are not sold in this period. They are returned to the producer with a fine. 4. Transportation of products between the manufacturer's origin and retailers’ costs. 5. Transportation of products from retailers to different markets has shipping costs. 6. Transportation of goods between different retailers’ costs. 7. Returning products from retailers to the origin of production costs. 8. The initial inventory level is zero and the inventory of the end of the last period is considered zero too.

The variables and parameters are defined as bellow:

Product counters i: 1, .., I

Retailer counters j: 1, .., j

Destination Counter (Market) s: 1, .., S

Count of time intervals t: 1, .., t

Model variable are defined as bellow

The number of ith products delivered to the j-th retailer during the time period t. Xijt

The number of i-th products sold during the time period t by the jth retailer in the sth market. Yijst

The number of i-th products that are sold to retailers j in the time period t from the jth retailer. Zijj't

The number of type I product that is returned to the manufacturer in the time interval t.

P(ijt)

Model notation are defined as bellow

The market demand for the ith product over the period t Dist

The cost of transportation a unit of product i from the manufacturer to the retailer j at the time t

CTijt

The profit from the sale of each ith product unit by the jth retailer in the market s and in the t-th period BNijst

The discount rate on the sale of each i-product unit for the transfer from the j-th retailer to j's at the time t ijj't

The penalty cost for returning each unit of the product I by the retailer j to the manufacturer within the time period t ijt

The cost of transferring each i-th unit from the j-th retailer to the market s during the time t CDijst

The cost of transferring each i-th product unit from the j-th retailer to the retailer j's in the time t CBijj't

The return cost of each product unit i by retailer j in the time interval t CRijt

Retail capacity j CPj

Rate of reduction in the price each i-th product unit in the time t it

Model formulation

The mathematical model presented in this study is a nonlinear mixed integer programming model. This leads to attention to the use of Metaheuristic algorithms. On the other hand, the results of the literature review show that about 80% of the researches in this field have used Metaheuristic algorithms for similar models.

The objective function of this model is to calculate the amount of profits from the sale of products by retailers. The first sentence is the amount of sales profits after deduction of the cost of transportation to the destination. The second sentence is the cost of transporting the origin of the produce to the grower's place. The third sentence shows the cost of the auction in the retailer, and the last sentence indicates the amount of redistribution and repatriation from the distributor to the original origin. The first limitation of the model shows that the total number of imported products of type i from all retailers to a market in each period should not exceed the demand for that market. The second limitation ensures that for each retailer the sum of the quantities sent from one type of product to all markets, plus the quantities sent to other retailers at the next auction for the auction, and the amounts returned in the two subsequent periods with fines must be equal to the values Receive from the manufacturer. The third limitation shows that the amount of product receipt for each retailer in each period is less than the capacity of the retailer, this capacity can be expressed in terms of storage space or available capital amount. The fourth limitation is for those who indicate that less than 20% of the products in each retailer in the next period can be auctioned and 80% of them should be sold on the market. This restriction, usually imposed by manufacturers, is aimed at encouraging retailers to sell more. The fifth limitation is similar to the previous limitation to prevent more than 30% of the goods received from the manufacturer from being damaged. Next limits (sixth, seventh, and eighth) are the logical constraints for the given commodity and the auction in the first and second periods because logically, the goods cannot be returned or auctioned in the first period. The last four limitations represent the scope of the variables of the model.

Contribution of the model

As already mentioned, the mathematical model presented in this study is followed by mathematical models that have already been presented by other researchers.

Choosing an appropriate metaheuristic algorithm for solving problem

Each of the metaheuristic algorithms has unique characteristics and features that speed up the search for the feasible solution space. In this research we will use the genetic algorithm. The reasons for using the genetic algorithm are:

1. This algorithm has been used repeatedly in similar models.

2. This algorithm utilizes a mutation operator to jump from local optimization points.

3. This algorithm can provide convergence by using the cross-over operator.

The following figure shows the performance of a classical genetic algorithm

The steps in this algorithm will be listed as follows:

Step 1: At this point, the inputs of the algorithm will be entered. The main inputs of the genetic algorithm used in this research are:

• Number of generations

• Number of members per generation

• Rate of jumps

Step 2: At this stage, inputs of the mathematical model will be entered. Which include:

1. Number of products

2. Number of retailers

3. Number of planning courses

4. The number of markets

5. The demand for each period (triangular function)

6. transportation costs from the manufacturer to each retailer

7. The cost of shipment from retailers to each market

8. The cost of returning the goods

9. The cost of carriage between retailers (at auction)

10. Rate of reduction of products

Step Four: Cross-over Operator

The operator selects the products in priority (sales profits) and selects them for transfer to retailers. In the future, these products are transmitted from retailers to the applicant's markets. This operator selects the product, retailer, and market of the applicant in such a way that the most benefit from the producer.

Step Five: Calculate the target function

After assigning the algorithm, the amount of the target function is checked to determine if this allocation has improved the model. In other words, does the algorithm have a tendency to accept a new answer?

Step Six: Mutable Operator

If, after assigning different products to retailers and then target markets, the response from the target function was not improved. The genetic algorithm with the probability of this allocation is allocated in the hope of better improvements in the process of the process. Although the probability of this allocation is very low, however, it is necessary to use it to cross the optimal local points. The amount of nerve jumps will be determined by a table.

Step 7: Exit the search algorithm

In this step, the genetic algorithm examines the exit conditions of the search process, and if these conditions are met, the algorithm stops, and the best answer is shown. Each of the above steps is fully explained, the mathematical form is shown, and the appropriate rates are chosen.

number of generations

The number of generations in the genetic algorithm actually represents the number of repetitive algorithms for improving the chromosomes of community members in different periods. Obviously, the more generations to be considered, the higher possibility of getting better answers, but it should be noted that, the higher volume of generations of an algorithm increases the problem-solving time and may lead to inefficiency of the algorithm. Therefore, proper selection of generations is necessary. For this purpose, the problems studied in this chapter are divided into three groups of small issues (having less than 25 variables), middle class issues having more than 26 variables and less than 100 variables, and large group issues with dimensions of more than 101 variables. Below for each of these value different numbers of generations have been considered and the results have been processed. The best values of generations for each category have been obtained as below table (Table 4-1).

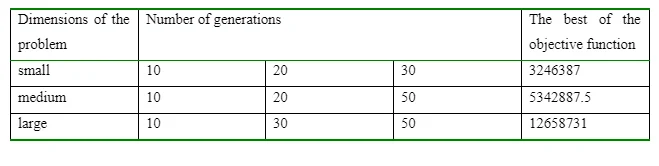
As you see the best number of generations will be 10 generations for small-scale issues,20 for medium size issues, and 30 for large size issues.

The number of members of each generation

Community members in every generation is an important factor in the nswer improvement. The greater the number of members of the community in each generation, the wider the range of searches and subsequently the better chance for better answers. But similar to the number of generations, taking large numbers for this factor will also increase the solving time and possibly the inefficiency of the model. The following table has been developed to estimate the appropriate number of community members in small, medium and large dimensions.

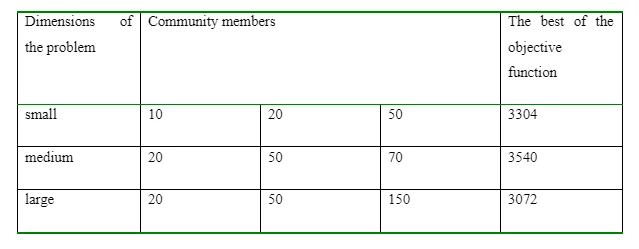
Similar to what was obtained for generations, the estimated value for issues with small, medium and large dimensions was considered 10, 20, and 50, respectively.

Operators estimate the demand for each product in each period

One of the features of the mathematical model presented in this research is to consider the probable demand of products. This feature helps the realization of the model, because in reality, the demand for fashion goods market is usually not predictable and is subject to many different factors that are beyond the scope of this research. For this reason, triangular distribution function has been used to estimate the demand for products.

It is noted that delta and gamma values are estimated by the market study and can be different for each product. But alpha and beta values that indicate the increase or decrease in demand estimation can be considered based on the decision maker opinion.

Calculate fitness function

After generating a result, to determine how efficient it is, it should be compared to. In this research, as in most similar researches, the objective function presented in the model will be used as the fit function. This operator function is such that the amount obtained from objective function is being compared to the best result from the objective function in the searching space so far. If the amount obtained from the current level is better than the previous, it will be used as a solution in the next generation.

cross-over operator

The purpose of this operator is selection of genes in the chromosomes. For such purpose, if a market is selected at a single stage in each generation and increases the fitness function, then the chance for being chosen for future generations will increase. In addition, in each period, 2 responses are selected as inputs, and their valuation would be done product by product. and the one with better result is located at the location of the relative gene in the chromosome.

1) Choose two parents. 2) Find their chromosome string. 3) For each gene in the chromosome string, calculate the improvement of the fitness function. 4) To choose a gene, pick the one in parent that results a greater improvement rate.

Mutation operator

1.Consider a number as the mutation rate (Fig. 4-5). 2. Calculate the fitting function for a new generated member and compare it to the best value obtained from objective function. 3. If the amount of fitting function calculated for a newly generated member is less than the objective function, then accept the answer with the probability of a mutation rate. 4. Otherwise, reject it.

Table 4-3 that is a sample for small-dimensional problems, shows that the best value for the mutation rate for small-dimensional issues is considered as 0.1. Similarly, the rate for medium and large-scale problems will be considered as 0.1 and 0.3 respectively.

Conditions for stopping the genetic algorithm

Genetic algorithm would stop searching in the solution space when one of the following scenarios occurs:

1. The number of generations will be fully spent. 2. If more than 30% of generations do not succeed progressively. For example, if the number of generations is 100, then the search stops when the algorithm does not see any progress in 30 successive generations.

SOLVING NUMERICAL EXAPMLES AND ANALYZING RESAULTS

In this section, numerical examples will be solved to demonstrate the validity and performance of the proposed algorithm. these numerical examples are designed to accommodate the different. In this situation, we shall consider the problem in small, medium and large-scale categories. Our aim is to illustrate if this algorithm is appropriate to solve problems in large scale mode or not. We assume that example ranges start from 5 products, 5 retailers and 5 target markets to 100 products, 30 retailers and 30 target markets. As the main reason for using meta heuristic models is their speed in searching the solution space and reaching to acceptable result, the computer specifications being used should be specified, as the CPU, RAM and processor type will certainly be very effective on computer speed. In this study, a personal laptop with an Intel® Core ™ i5 processor with 2.50 GH CPU and 4 GB RAM being used. By applying the model on various numerical examples, different results have been obtained. Below we will analyze the different results. 1-As we can see, the developed genetic algorithm is able to solve all numerical examples in different dimensions and with different inputs. Therefore, using this algorithm seems to be appropriate 2-The results show that the proposed genetic algorithm can solve small, medium and large dimensions in logical time intervals (based on the problem dimension). 3-The results show that the results obtained in the first generation up to the last generation in the algorithm have been improved by the range of 3% to 28% in different examples. Therefore, it can be concluded that the developed genetic algorithm has a good ability to search to the optimal path. 4-Comparing the results of genetic algorithm with forwarding serial planning method shows that the developed genetic algorithm has given better result and is able to make much suitable improvement. This means cross-over, and mutation operators have good functionality. 5-The results of the studying the conditions of constant demand with the probable demand indicate that when market demand is probable, the amount of profit is highly affected by this difference and can be up to 40% (in the examples solved in this research) depending on the probable rate of change market slowly. This issue is very important and should be considered in different markets.

Verifying the model using a practical example

In this section, to verify the operation of the model in the real world, information from a company manufacturing aluminum component located in Alborz province has been collected and used. The company sends 5 aluminum products to its four retailers in the provinces of Tehran, Alborz and Qazvin. These retailers sell their products in each of these three provinces. It should be noted that the sample numbers have been slightly modified according to the manufacturer's request.

The rest of the example information is shown as follows

Demand in various markets for these products were estimated using MATLAB:

Also, the capacity of retailers is as follows:

The remaining parameters of the genetic algorithm are considered as follows:

• Number of generations: 10

• Number of members of the community: 10

• Mutation rate: 0.1

After solving the model, the overall result of the model was obtained as follows:

• Resolved time: 1.6 seconds

• The amount of target function achieved: $ 3241

The complete solution of the model by genetic algorithm is shown below:

Part I Response:

The received amount of each type of goods produced by the retailers. This type of categorization can be considered different from the decision maker based on circumstances of the retailers (such as geographic location, population distribution, etc.).

Part II Response:

from different retailers. This is done in such a way that, firstly, the minimum shipping cost is considered, and secondly, this amount wouldn’t increase the amount of goods that the retailers have received. As the above table shows the delivered goods from any retailer does not exceed the capacity that has been considered for them. But from the comparison of the above table and the previous table, it can be concluded that some retailers still have a high proportion of the products produced, with surplus amounts being auctioned in the next period. As with mathematical symmetry development, none of these values should exceed 0.2 of the amounts of goods received by the retailer. For example, for the first retailer As the table above shows, 10 of the third type goods, 7 of the fourth type goods and 3 of the second type goods, these values should be sold in the auction market. Table 4-12 shows these values for the subsequent period. As can be seen, in the case of the first retailer, all surplus products can be sold at auction. But with regard to the second, third and fourth retailers, due to the surplus of more than the products in the warehouse, all these quantities cannot be auctioned on the market, so the residual products with a drop-in value are returned to the producer. The remained products at retailer may get thrown away because of non-return acceptance by the producer. It should be noted that if we consider 1 for the rate of goods return, that means all the products that hasn’t been sold or auctioned, and for the rate of 0 none of the goods at such state would get returned to the producer and so will be thrown away.