The Importance of Graphs in Analyzing and Presenting Data

Section 1: Introduction (The impact of good and bad graph and table)

A diagram (Graphs and tables) can make it less demanding to break down and translate the data you have gathered, particularly quantitative information. If you need assistance, seeking quantitative dissertation help can provide valuable insights. Graphs are perfect for imparting logical data. There are a wide range of sorts of Graphs. The sort of diagram utilized relies on upon the kind of information that has been gathered. The chart beneath delineates the fundamental elements of a graph. Graphs are just on a par with the information they display. No measure of innovativeness can create a decent diagram from questionable information.

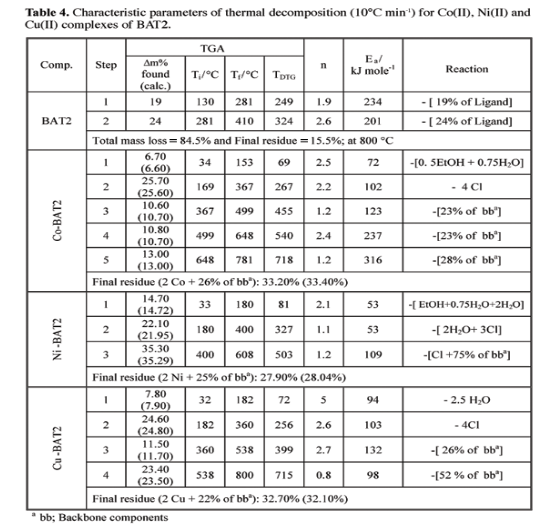
This table (Figure 1) is used by (Al-Maydama et al., 2008) in their journal for representing the characteristic parameter of thermal decomposition.

However a table is used mainly when the author tried to be sorted out the information so that the implying that the creator is attempting to convey is clear. For the most part, it is of more enthusiasm to look at estimations of a similar variable in various populace units than to analyze estimations of various factors for a similar populace unit. The problem of this table is that the table is very complex in nature. A table always should be enough simple that it will describe the whole information at a glance. For specifically this table, the writer tried to too many information in one table, but he may be forget that a table should use to understand the information without any difficulty.

Solution

The best solution is to use more than a table as too many information is one table make it more complex. For each component (Cobalt, Nitrate, Coper), one table should be perfect to understand the table. That’s why instead of one table, 3 tables is recommend to make the information easier to be understood.

This graph is built for understanding opportunities Closed-Lost of a company with its revenue according to every month.

Graphs ought to be not any more mind boggling than the information which they depict. Diagrams ought not to give a contorted photo of the qualities they depict.

Graphs work best when the information introduction:

Is utilized to impart a message that is contained in the state of the information

Is utilized to uncover relationship among many qualities

Is utilized to make a point from the data.

However for this graph, closed lost opportunities is visualized by an area column chart in such a manner which is really complex to understand. The author wanted to depict its quarterly opportunity lost also but then he added revenue over the month and the bar chart of revenue over the month covered its quarterly opportunity lost. That’s why the graph become a hazard.

Solution

The author can use just simple clustered column chart with 2 series (Series 1: revenue, Series 2: closed lost opportunities) and with 4 categories (category1:1st quarter, category 2: 2nd quarter, category 3: 3rd quarter, category 4: 4th quarter). This is highly recommend for use as this will be chart and easily understandable.

Section 2:Introduction(A study on the impact of Easter Revision Programme in GCSE score)

The present research is conductedin order to determine the impact of a program of Easter revision in helping students prepare for their GCSEs (age 16 public exams). For this reason, surveys had been done to compare the Average score across English, Mathematics, and Science at GCSE (GCSEAVSC) between the students who attended the revision program and vice versa. Other than that various factors like student’s motivation to learn of student (MOTIVATE), Gender (GENDER), Average performance at age 11 in national tests for verbal and non-verbal reasoning (NFERAV), Score in a Mathematics test at age 11 on starting secondary school (MATHTEST) all are analyzed with the view of understanding the influence of these factors on the score.

Aim of the research

The primary aims and objectives that this study proposes to achieve are:

To determine and understand the effects of Easter revision program on the score at public exam in (GCSE).

To determine and understand the impact different factors like motivation, the score of 11 exam on the score at public exam in (GCSE).

Context of the research

The background of the research is to understand different factors and to search the principle factors which are responsible behind the score of public exam of the students of mixed-sex comprehensive schools in Southampton. For this, students who have got the score of public exam, are only eligible for the survey.

Method

Participants

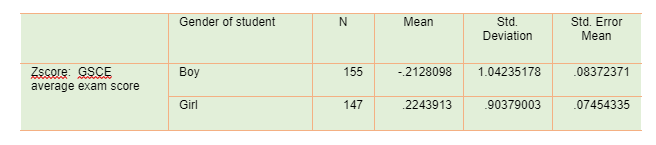
As per the data, there were a total for 302 (Figure 3) participants. 51.8 percent (155) of the participants were boy while remaining 48.3 percent (147) of the participants were girl. All information are collected from the students of mixed-sex comprehensive schools in Southampton. This sample should be viewed as a random sample of all students of the relevant age in Southampton. Around half of the pupils in the study attended the revision program. Data collection was done by research assistants. All applicants provided informed consent about their participation. As gender can be a vital factor that’s why data are gathered from mixed mixed-sex comprehensive schools.

Study Design

The study was quantitative in nature. The design of the questionnaire is one of the most difficult and strategic work to do as it was done for collecting proper information. This experiment used a between-subjects design. To interpreting the effect on the scores, the score of GCSEAVSC is the independent variable of the research and the dependent variable is mainly attendance of the in the Easter revision program and other than that GENDER, NFERAV,MATHTEST, MOTIVATION , all are also dependent variable. For standardization, dummy variable are used to get perfect result.

Procedure

After the collection of data, at first descriptive analysis was done to understand the data and visualizing it properly. The standardize mean difference is utilized as an outline measurement in meta-examination when the reviews all survey a similar result however measure it in an assortment of ways. In this condition it is important to institutionalize the aftereffects of the reviews to a uniform scale before they can be consolidated. After standardizing, primary aim of the data is to determine and understand the effects of Easter revision program on the score at GCSE. For fulfilling the aim, mean of score of attendant and non-attendant students are compared. After this, the relationship between other variables like GENDER, NFERAV, MATHTEST, and MOTIVATE with the new variable standardized score of GCSE are explored. Attendance is one of the important variable in the model. For exploring the association between categorical variable Attendance with other categorical variable gender and continuous variable MATHTEST, regression cannot be performed as the dependent variable categorical. So, logistic regression is performed for exploring the association between categorical variable with other categorical and continuous variable. A simple bivariate regression was done to understand the impact of attendance and the score of Math-test on GCSE score. As the attendance variable is categorical in nature so dummy continuous attendance variable is created for performing simple bivariate regression. One of the assumption of simple bivariate regression is that all variable have to be continuous in nature. MATHTEST and NFERAV both are test scores of the student. To judge the impression of both variable are same or not, simple bivariate regression is done. A combine variable of both also used to understand. As the combine variable is used in linear regression that’s why multiplication method is chosen. Cronbach alpha’s score of reliability test was done to check two variables are on the same scale. All categorical variables are converted into dummy continuous variable and all continuous variable are standardized. Then regression model containing all explanatory variables is analyzed and multicollinearity test was also done. From this, insignificant variable is removed and lastly final model is generated and its residuals are tested for understanding the goodness of fit of the model.

Question 2: To investigate the difference in mean scores of the standardized variable between those students who attended the revision programme and those who did not.

After the standardization of the scores in GCSE, means compares for determining the impact of the categorical variable attendance on the score the students in GCSE.According to the result (Figure 4), the mean Z score of students who attended the Easter revision program, is .41 and the mean Z score students who not does attended the Easter revision program, is -.389. Two means are not same. There is a significant difference between two means. It depicts that the difference in mean scores of the standardized variable between those students who attended the revision program and those who did not. The positive standardized mean value of attended students and the negative standardized mean value of non-attended student reported that attendance in revision program had a great impact on the national GSCE scores.

Question 3: To explore the strength of association of the other variables (GENDER, NFERAV, MATHTEST, and MOTIVATE) with the standardized version of GCSE score

T-Test for checking the equality of population mean z_GSCE score of boys and girls

According to the Group Statistics box (Figure 5), standardize mean score of girls is .224 which is higher than -.212, standardize mean score of boys. It seems to be that girls are doing well than boys. Levene’s Test for Equality of Variances significant value is .051 which means there is no significant variability between gender and standarize GSCE scores. ). The table (Figure 6) shows that the p-value or the significance value of the analysis comes out to be 0.000, which is lower than 0.05. It means that obtainable null hypothesis is rejected and the alternative hypothesis is accepted. That is, there is statistically significant difference between gender and standarize GSCE scores.

Correlations between Z_GCSE score and Math-test

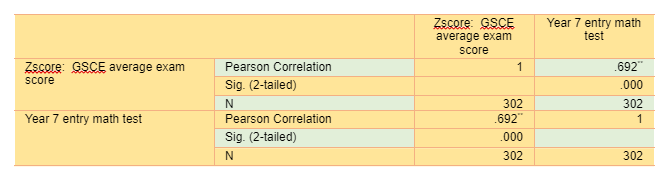
According to correlation table (Figure7) a strong positive association between standardized Z score of GCSE and score in a Mathematics test at age 11 on starting secondary school has been resulted. When Pearson’s correlation value is greater than 0.5 and close to 1, it depicts a strong positive correlation between two variable. In this case, the correlation value is reported .692.Significant value (2 tailed) is .000 which is lower than .05, depicts that there is a statistically significant correlations between two variables. So, it seems to be concluded that changes in standardized Z score of GCSE variable are strongly correlated with changes in the score in a Mathematics test at age 11 on starting secondary school variable.

Correlations between Z_GCSE score and NEFRAV

According to correlation table (Figure 8) a strong constructive association between standardized Z score of GCSE and Average performance at age 11 in national tests for verbal and non-verbal reasoning has been resulted. In this case, the Pearson’s correlation value is testified .723.Significant value (2 tailed) is .000 which is lower than .05, depicts that there is a statistically significant correlations between two variables. So, it seems to be concluded that variations in standardized Z score of GCSE variable are strongly correlated with variations in Average performance at age 11 in national tests for verbal and non-verbal reasoning. It meant that Average performance at age 11 in national tests for verbal and non-verbal reasoning have great impact on standardized GCSE score.

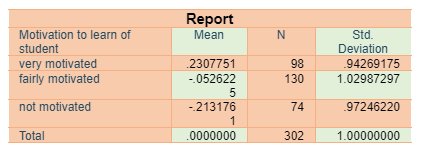
Comparison Z_GSCE score of 3 types of motivation

The case processing summary of motivation in the context GSCE score value, it is resulted the motivation of learning where 98 students are very motivated, 130 students are fairly motivated and 74 students are not motivated. According to the result (Figure 9), mean of very motivated students is positive (.230) mean of fairly motivated students and not motivated students are negative (-.052, -.213 respectively). Simply it depicts that motivation have positive impact on GSCE score which means if motivation is high then score will be high.

Question 4: Explore the association between attendance and categorical variable GENDER) and one continuous variable MATHTEST

For evaluating association between attendances variable with other categorical or continuous variable, simple regression or correlation method are not valid. As attendance variable is dependent variable which categorical in nature, so logistic regression can be performed. Simple regression can be done when dependent variable is continuous. That’s why caution is needed when the attendance variable is measured. In question 2 same case was happened as attendance, categorical variable is measured against GSCE score which is a continuous variable.However independent variable of logistic regression is can be categorical or continuous. So it can be concluded that for exploring the association between attendance and GENDER and MATHTEST, logistic regression can be performed.

However for better understanding the variable attendance, logistic regression was performed mainly for evaluating relation between attendance with respect to gender and math test. The table (figure 10) contains the Cox & Snell R Square and Nagelkerke R Square values, which are both methods of calculating the explained variation. Therefore, the explained variation in the dependent variable based on the model ranges from 8.5% to 11 %, depending on whether to reference the Cox & Snell R2 or Nagelkerke R2 methods, respectively.

Question 5(I): To explore bivariate regression model relating the standardized value of GCSE score with the attendance variable

The R value (Figure 11) represents the simple correlation and is 0.400, indicates a positive correlation. The R2 value indicates how much of the total variation in the dependent variable standardized GSCE score, can be explained by the independent variable, attendance. In this case, 15% can be explained, which is not bad. Significance value of the regression model is .000 which depicts that the dependent variable statistically significantly predicts the outcome variable which means that attendance have good impact on GCSE score. In question 2, it proved that attendance in revision program had a great impact on the national GSCE scores. So in both cases similarities are found. Both case signified the relation between attendance and the national GSCE scores.

Question 5 (ii): To explore bivariate regression model relating the standardized value of GCSE score with the attendance and MATHTEST variable

After adding the variable MATHTEST (Score in a Mathematics test at age 11 on starting secondary school), the regression model has been altered. The R value(Figure 12) represents the simple correlation and is 0.724, indicates a high degree correlation. In this case, the R2 value is .524 which means that 52% can be explained, which is very good. Significance value of the regression model is .000 which depicts that the dependent variable statistically significantly predicts the outcome variable. After adding new explanatory variable, the explained percentage of model get improved which depicted that the score in a Mathematics test at age 11 on starting secondary school have high impact on GCSE score.

Question 6: To explore bivariate regression model relating the standardized value of GCSE score with the NEFARV and MATHTEST variable

To explore the impact of two explanatory variable NEFARV and MATHTEST against the dependent variable, simple bivariate regression has been done. New regression model has been designed after adding NEFARV variable to the prior regression model. New revised model have R value of .777 which is very high. Approximately 60% of standardized value of GCSE score can be explained by the 3 dependent variable according to R2 value of new model (Figure 13). Cronbach alpha’s score of reliability test between two NEFARV and MATHTEST variable for indicating internal consistency between two scales, is resulted .856. It depicts high level of internal consistency. The combined variable of NEFARV and MATHTESTvariable was added in the prior regression model instead of adding differently those two variables. According to the result, R value and R2value is .772 and .59 respectively (Figure 14). That means there are slight difference between using combined variable rather than single variable which is negligible. So both can be used. But for this case, both variable are chosen.

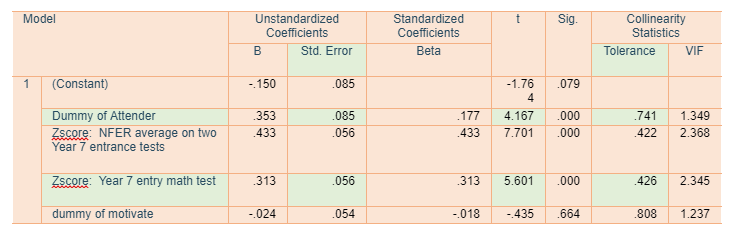
Question 7: Estimation of a regression model containing all explanatory variables

For exploring the impact on standardized GSCE score of all explanatory variables gender, dummy attender, standardized MATHTEST, standardized NFERAV and dummy variable of motivation, all are analyzed through linear regression. According to the result of model summary, this model is able to explain 62 % of the dependent variable which is quite good. For checking multicollinearity, a popular factor is the Variance Inflation Factor, which is just the reciprocal of the tolerance statistics. A VIF of greater than 5 is generally considered evidence of multicollinearity. According to the co efficient table all VIF are lied in 1-2.5 and it depicted that this model has no multicollinearity issue. The b coefficient of dummy of motivate -0.024(Figure 15) suggested that motivation factor is not working well and respective significant value is .808 which is higher than 0.05 and depicted that the independent variable motivate is not contributing statistically significantly to the model. So motivate variable is removed.

Final Regression model:

Hence the final regression model is designed with the standardized GSCE score, dependent variable in respect to the independent variable gender, dummy attender, standardized MATHTEST, standardized NFERAV. This model is this model is able to explain 62 % of the dependent variable and only statistically significant independent variable which contributes to the model are added (Figure 16).

Model 1 = Final model; Model 2 = regression with Attendance and MATHTEST; Model 3= regression with Attendance

The regression equation (Figure 17):

Z_GSCE score = -6.403+.233gender + 0.035NFER +0.025 MATHTEST +.353dummy_Attender

According to the final regression model, strongest predictor is attendance as 1 point increase is associated with a .353 point increase in GCSE score. Other than attendance, gender has also great impact on GCSE score. According to the model, effect of Average performance at age 11 in national tests for verbal and non-verbal reasoning is slightly high than the impact of Score in a Mathematics test at age 11 on starting secondary school.

Improved R2 is best known for detecting the goodness of the model. The adjusted R squared increases only if the new term improves the model more than would be expected by chance and it can also decrease with poor quality predictors. The R2 of the final is high than other model. So it seems to be that data is fitted well.

Question 8: Final regression model with residual plot

Normality of the error distribution:

One of assumption of the bivariate regression model is that the residuals (errors) of the regression line are approximately normally distributed. The scatter plot is good way to check whether homoscedasticity (that is the error terms along the regression are equal) is there in the error terms or not.

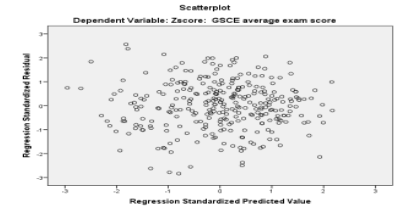
From this figure, it can be concluded that the residuals are symmetrically distributed, tending to cluster towards the middle of the plot.in general, there are no clear pattern is showed. So residuals are normally distributed.

Discussion

The above analysis was performed to determine the impact of attendance in Eater revision in the students GCSE score. According to the result there is significant difference between mean of two groups of who attended to the revision program and who doesn’t. However other variables like MATHTEST, GENDER and NFEARV all have significant impression on standardize GCSE score. Association value of NFERAV with GCSE score is resulted slightly high than association value of MATHTEST with GCSE score. It also proved later in final regression model that NFERAV has slight more impact on GCSE score. From the simple regression model of dependent variable GCSE score in the context of independent variable attendance is resulted that 15% of GCSE score can be explained by attendance when MATHTEST is added to the same model then 52% of GCSE score is explained by it. So Attendance and MATHTEST are both are the major component of Attendance. Combined variable of NFEARV and MATHTEST are also designed to recognize the effect of combine variable. However by regression is resulted that both independently contributes to the model. B coefficient of dummy of motivate -0.013 suggested that motivation factor is not working well. After checking multicollinearity, that’s why motivate variable is removed and final regression model is designed after checking its residuals. According to the final model, strongest predictor is attendance and NFERAV, MATHTEST and gender are also contributes significantly to the model. Hence at last it can be concluded that there is a high impact of attendance in Eater revision in the students GCSE score.

Appendix

Continue your exploration of The Impact of Technology and Globalization on Retail Strategies with our related content.