Practical Application of Two-Factor ANOVA

We have looked at the general principles behind two factor ANOVAs. Now we need to follow through the examples for the different designs using ANOVA on made-up data, so that you can see the three relevant F values and learn how to extract information of the SPSS printout. For more detail of how to input the data for each design into SPSS, and how to run the correct analysis, please look at the relevant sections in the Dancey and Reidy or any other SPSS book you may have. If you require further assistance, consider seeking statistics dissertation help. A few brief SPSS instructions are given here e.g., for split plot design.

1. Two between-participants factors

Recall for this design we are using the Naming experiment where different groups of participants learnt the names of famous faces either as actor only, actor + character and actor + series name (Learning Factor). Young and old adults were tested (Age Factor), making this a two factor between-participants design. After the Learning phase, they then had to name all the faces in the experimental phase, and naming times were measured.

To input the data, you would need a different line for each data point, as shown above. This is because this design has different participants in every condition. You would also need to carefully code each piece of data for the Learning conditions (Codes 1,2 and 3), and also for the Age conditions (Codes 1 and 2). See how each data point therefore has two codes. For example, participant 3 above was in the Actor + Character condition (code 2 for Learning factor) and in the younger adult group (code 1 for Age factor). It is possible to give labels for these codes in the Values column, in SPSS, to help you remember what they refer to.

You are now quite familiar with carrying out basic SPSS analyses, so please refer to Dancey and Reidy to see how to do input data and run analyses.

However, a very brief summary of a two factor between participants ANOVA instructions for SPSS follows.

SPSS instructions for two factor between participant ANOVA

Go to Analyse, then General Linear Model, then Univariate.

Move the DV label on the left to the box for DV on the right

Move the two factor labels from the left to the Fixed Effect box on right

Go to Options. Take everything from the left over to the right box. Tick descriptives.

Click on Plots. Take Factor 1 (e.g., learning) to the “horizontal axis”. Take the other factor (e.g., age) over to “separate lines”

Click Add. Then Continue, and you should get your printout on screen.

Here is the relevant bit from the printout of results from this two-factor between-participants design, using data I have made up.

SPSS Print Out of results Face Naming and Age experiment from Lecture 2.

Between-participants Factor 1 = Learning condition (Actor, Actor + Character, Actor + Series)

Between-participants Factor 2 = Age (young, old)

Dependent variable – time to name faces in experimental test

Extracting the F values and writing them formally

Now you must find the three relevant F values (two main effects and the interaction between the two factors), and report them formally as before, using the relevant degrees of freedom for the factor that is being tested, and then the df for the error term.

1. The test of the main effect of the Learning factor (the first factor)

From the ANOVA table, the main effect of Learning condition is significant, F(2,24) = 14.20, p < .001

This indicates that overall, there is a difference in naming times as a result of the manipulation of the Learning conditions. You would now look at the marginal means for the Learning conditions. These were obtained from SPSS by going to Options when you running the ANOVA, and taking all the variables from the left box over to the right box (see above instructions). Or you could work them out by hand, like we do in the lecture!

Estimated Marginal Means for Learning/Practice factor:

Remember that each of these marginal means averages over the two Age conditions. From these means, we can see that Condition 1 (Actor only), leads to faster naming times for the famous faces relative to Condition 2 (Actor + Character). The mean for the Actor + series name falls between these two conditions. We don’t at this point know which of these means differ significantly. From the significant main effect result, we only know that at least one pair of these means differs. I will later indicate how to carry out follow-up comparisons after a two factor ANOVA if necessary.

2. Now for the main effect of Age (the second factor).

Main effect of Age is F(1,24) = 40.68, p < .001

So, there is a significant difference between the Young and Older adults.

Again, you would look at the marginal means (use Options in the ANOVA procedure):

Clearly, the older adults take longer to name all the faces than the younger adults. Because there are only two levels to the Age factor, you can simply look at the two marginal means, and see where the difference is. You do not need to do further tests.

3. Now we must look at the test of the interaction between the two factors;

Learning * Age F(2,24) = 6.798, p = .005

So this means, as we already saw on our graph in the previous lecture, that the effect of the Age factor is not the same at each level of the Learning Factor. I have printed the graph again, and so look at this, and also look at the six individual cell means printed from the ANOVA below. These are the means used for the graph.

Remember how we commented before that the effect of the Learning factor appeared to be stronger for the older adults (top line) than for the younger adults.

Note that because the interaction is significant, this “qualified the interpretation of the two main effects”. You have to look at the individual cell means to see what is going on. The graph helps, but you can do “follow up tests” to explore the interaction further. These are called simple effects, and we may cover these in a later lecture.

There are two possible ways to do these simple effects, and a separate handout will be prepared for students who want to have a go.

In a write-up, after you have reported any significant results from an ANOVA, it is your job to then interpret the results fully in the Discussion section. Below is a summary of what you need to do in a 2 factor experimental design results section, but you can look in Dancey and Reidy for examples of results sections.

Results sections

1. State what the data are (e.g., average response times for each condition), and whether any data were excluded

2. Present table of descriptives (mean, sds, for each condition) and comment briefly on pattern in data.

3. State what ANOVA carried out, and report the results of this succinctly (the 3 F values, formally presented). Be clear which direction the effects are i.e. in which condition are scores higher relative to other conditions? It is helpful therefore to report the marginal means, when reporting the main effects (e.g., put marginal means in brackets after reporting main effect).

4. If interaction significant, useful to present a graph, and refer to the nature of the interaction, with reference to graph. Again, be very clear about the direction of effects.

5. If interaction is significant, and you are confident, carry out simple effect analyses (see later handout/powerpoint).

2. Two within-participants factors

You have now seen how to extract, understand and write the three F values for a two factor between-participants design. It is the same principle with other two factor designs, although the SPSS print outs will look different, and there will be more than one error term when there is at least one within-participants factor.

We will look briefly at a printout from a two-factor within-participants design, using made up data for the Face Semantic Priming and Interval Example 2 we used in the last lecture.

Recall that in the face priming experiment, participants were given target faces, which were either preceded by an associated prime, a prime from the same category as the target, an unrelated prime, or a neutral prime. This was the first within-participants factor. The stimuli were either presented with a 50 ms interval between prime and target, or a 1000 ms interval. This was the second within-participants factor. Participants had to make judgements as to whether the target face was a familiar face or not (this is the dependent variable), and so the experiment also included unfamiliar (unknown faces) as well as famous faces, which we will consider as just filler stimuli (The responses to unfamiliar faces were not analysed, though, only the responses to familiar faces).

So, considering just the familiar experimental stimuli, there are now two manipulated within-participants factors, with 8 conditions altogether. The researchers would be interested in whether the effect of the prime was different according to the interval between prime and target.

Factor 1 = Prime type (associated, category, unrelated, neutral)

Factor 2 = Prime-target interval (50 milliseconds, 1000 milliseconds).

DV = reaction time to make familiarity decision

The data for each participant would be entered in SPSS all on a single line. You would need to specify the conditions in SPSS using variable names. For details of how to enter the data, and how to carry out a two factor within-participants ANOVA, you must follow the Dancey and Reidy chapter. Here we will just look at the printout.

SPSS Print Out of Priming and Interval experiment

First, since we have 4 conditions in the Prime within-participants factor, we must check the Mauchly test (see previous lecture on one factor ANOVA – the Additional Notes). Here it is.

You should see that the Mauchly test for the prime, factor and the Interval * Prime interaction just fail to reach significance. We might be wise, though, to use the Greenhouse Geisser adjustment (see Lecture on one factor within participants ANOVA and the Additional Notes), when we write the F value.

Now we can look at the results below of the two factor within-participant ANOVA. Remember there are bits on the within printouts that you can ignore.

Exercise 1 - two-factor within-participants ANOVA printout – Face Priming and Interval example (see answers later).

1. Write down the results to the test of the main effect of the Interval Factor. Give relevant marginal means. (use sphericity assumed row because this factor has only 2 levels so sphericity not an issue). What does the result indicate?

2. Write down the results to the test of the main effect of the Prime Factor. Give the relevant marginal means. Use the Greenhouse Geisser df. What does the result indicate?

3. Write down the results for the test of the interaction between the two factors. Is the interaction significant? Plot the individual cell means on a graph just so you can see what the results look like.

4. What do the results show overall? Do you need to do any follow up tests? If so, what would you suggest doing? (see also later lecture on follow-ups)

Answers - Exercise 1 - Face Priming and Interval – two factor within-participant printout

1. The main effect of Interval was significant, F(1,9) = 8.23, p = .019. The marginal means tested for this factor were 829.75 for the 1000 ms interval (Condition 1), and 793.28 for the 50 ms interval (Condition 2). The result indicates that overall, participants took longer to judge the faces as familiar in the longer interval.

2. The result for the test of the main effect of the Prime factor was F(1.814, 16.322) = 23.59, p < .001. The marginal mean for associated primes (Con 1) = 759.70, for the categorical prime (Con 2) = 790.20, for the unrelated prime (Con 3) = 890.15, and for the neutral prime (Con 4), 804.00. The results indicate that participants were able to make familiarity judgements to target faces preceded by an associated prime more quickly than to the other conditions. The mean for the Unrelated prime condition is the slowest response time of the four conditions.

3. The test of the interaction between the two factors was significant, F(1.861, 16.752) = 20.28, p < .001. There was therefore a significant interaction between the Interval and Prime factors. The Excel graph below plots the individual cell means (see printout above for these).

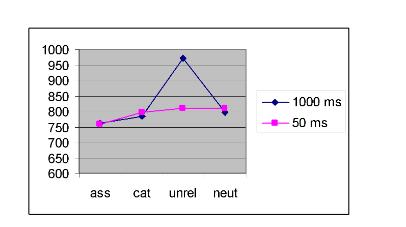
The graph helps us to get a handle on the interaction. We can straightaway see that the effect of priming is different for the 50 ms and 1000 ms levels of the interval factor, and that it appears to be the Unrelated condition which is causing the statistically significant interaction between the two factors. When primes and targets are separated by 1000 ms, the unrelated prime results in a considerable slowing of response times, and this is not the case for the 50 ms Unrelated condition.

4. Overall, the ANOVA table results show that both main effects are “significant” (unlikely to be due to sampling error), but these are qualified by a significant interaction.

Follow-up comparisons are needed. It would make theoretical sense to carry out simple effect analysis looking at the effect of prime conditions at the 50 ms interval, and then similarly, the effect of prime conditions at the longer interval. This could be done by getting SPSS to do a one factor within-participants ANOVA (see earlier lecture) on the priming data for the 50 ms interval, and then another ANOVA using the 1000 ms interval data. You could then see if both of these are significant.

If the ANOVA result was significant for the priming data for a particular interval, you could follow up further with specific related t-tests between pairs of priming conditions to see where the differences were (e.g., you could compare each prime condition against the neutral condition). However, given the number of comparisons, be sure to use a Bonferroni adjustment to the alpha level (see also Additional Notes on Follow-ups to one factor ANOVA).

3. One within-participants factor and one between-participants factor (split-plot design)

This design is sometimes called a split plot design. We will use as our example the face priming and task experiment from the previous lecture that we briefly referred to. To remind you:.

Young et al (1994) were interested in whether semantic priming might be different depending on what kind of decision you have to make about the face. One group of participants were asked to judge whether famous target faces were familiar or not (unfamiliar faces were of course included again like before, but we will regard these as filler stimuli). Another group of participants were asked to judge whether the target faces were female or not. All target faces were preceded by briefly presented prime faces, which could either be related, unrelated, or neutral. Reaction times were recorded. Let’s assume that only the responses to the familiar target faces were analysed, and further more, that only the responses to the female target faces were analysed – the rest of the stimuli were regarded as fillers (strictly these constitute part of another Factor, but we are ignoring that here).

Factor 1 – Type of prime – within-participants factor (related, unrelated, neutral)

Factor 2 – Type of task – between-participants (familiarity decision, sex decision).

The crossing of the two factors gives 6 conditions. It can be referred to as a 3 x 2 design.

Again, I have made up some data for this experiment. For this type of design, once again any data from the same participant goes on a single line in SPSS. However, because the study has a between factor, you must code each participant according to which task they did (1 or 2). The details of running the analysis can be found in Dancey and Reidy. I will give brief SPSS instructions here, which you should be able to use for any study. Here, I use some data for this particular face priming and task study. Here is some sample (made-up) data for this design (not the full set of data used for analysis and printouts, though).

Inputting the data in SPSS

In SPSS, in Variable View, you would set up a column for the between participant factor (Task), and then a column each for the three conditions/levels of the within-participant factor (Prime).

See for the between-factor Task how you need to use a code to tell SPSS whether the participant was in the Familiarity decision group (code of 1), or the Sex Decision group (code of 2). If you had 3 groups of participants, you would use 3 codes, of course. You can use the Values column in Variable View to spell out what these codes refer to, to remind yourself if you want. Having coded a participant for the between-participants factor, you then enter the data for the conditions of the within participants factor all on one line.

Running the split plot ANOVA

You then save the data if you want, and switch to Data View.

Ideally you need first to do exploratory data analysis, to see if data normally distributed, variances homogenous, outliers etc (see SPSS Exercise 1 handout in Week 1 on Moodle).

Here, though, are the basic instructions for split plot ANOVA.

Go to Analyse, then General Linear Model, then Repeated Measures.

Give a sensible name for the within participants factor in Factor 1 (e.g., Prime, for our example here). Specify the number of levels (e.g., 3, in this example)

Click on Define, and then in the new window, take all the within-participant conditions from the left box to the right Within-Subject Variables box.

Take the between-participant factor (Task in this example) from the left box to the Between-Subject box.

Click Options. Take everything from the left box to the right Display Menu box. (this will on the output give you the marginal means for the two main effect tests, and the individual cell means for the interaction effect).

Click on descriptive too (you will also get the standard deviations as well as means, usefully).

To get a graph, select Plots, and take the within-participants factor to the Horizontal, and the between-factor to Separate Lines.

Click Add.

Then Continue, and OK, and you should get your printout, as below.

UNDERSTANDING PRINT OUT FROM SPLIT PLOT ANOVA (ONE BETWEEN FACTOR, ONE WITHIN FACTOR)

Assume here that much more data were analysed than that given above in example.

There are several separate parts to this type of analysis that will be relevant.

We had a within-participants factor in our example above with 3 levels, so we need to check the Mauchly test.

First, below we can see below that the Mauchly test is not significant (p = .301), so the sphericity assumption for the Priming within factor has not been violated (see below). Good. We can therefore use the sphericity assumed row for reading of the within-participant factor results, and for reading of the interaction results.

NB : when you only have 2 levels for a within-participants factor, sphericity is not an issue, and you don’t need to even look for the Mauchly result. Just use sphericity assumed row.

Understanding the split plot ANOVA printout – see printout parts below

1. Notice that there are two effects reported under the source column in the separate box giving Tests of Within-Subject Effects. These two effects are: the test of the main effect of the within-participants Factor 1 (Prime in our example), and the test of the interaction between the two factors (Prime * Task ).

2. Notice that there is one main effect (between-participants factor Task in our example) reported under the source column for the separate box Tests of Between Subjects Effect.

3. Notice that there is one error term for the effects involving the within-participant factor, and a separate error term for the between factor.

4. Notice there are several rows to each within-subjects effect, one where sphericity is assumed, and three where it is not. If sphericity is OK (or irrelevant), then use sphericity assumed row to read off results. But If Mauchly test is significant, then when reporting your ANOVA F values, use Greenhouse Geisser row to read off results. In this example, the Mauchly was not significant, so use sphericity assumed. And if there are only 2 levels to your within-participant factor, then don’t worry about Mauchly, just use sphericity assumed.

We must also look to see if the between-participants factor which is included in this design is significant – see below – a different part of the print out.. You will see it is significant. So all three effects are significant.

Now we need the marginal means. Remember you can obtain these during the ANOVA by going to Options, and taking all the effects over from the left box to the right hand box. Here are the relevant bits of output/printout.

Estimated Marginal Means

Marginal means for the main effect test of the between-participants factor – the two Task conditions in this example

Exercise 2 – Split Plot ANOVA i.e. one factor between and one factor within ANOVA printout – face priming and task example given above (see answers later)

1. Write down the result formally for the test of the main effect of the Priming Factor. Give relevant marginal means. (you can use sphericity assumed row). What does the result indicate?

2. Write down the result formally for the test of the main effect of Task. Give the relevant marginal means. What does the result indicate?

3. Write down the result formally for the test of the interaction between the two factors. Is the interaction significant? Plot the individual cell means on a graph, by hand or using software. What does the graph indicate? Remember that Code 1 was familiarity task, and Code 2 was sex decision task.

4. What do the results show overall? Do you need to do any follow up tests? What could you do?

Answers to Exercise 2 - Face Priming and Task Factor example – one between and one within factor (also known as split plot design)

1. The main effect of the Prime factor was significant, F(2,36) = 17.27, p < .001. The marginal means are 687.90 for related prime condition, 716.65 for unrelated, and 713.50 for neutral prime condition. These means show that the related prime led to faster decisions to target faces compared to the other two conditions. There is little difference between the neutral and unrelated prime conditions. (In fact, you would need follow-up comparisons to check which pairs of conditions differed significantly).

2. The main effect of Task was also significant, F(1,18) = 22.16, p < .001. The marginal mean for the Familiarity decision was 792.03 and for the sex decision, 620.00. As there are only two means in this particular example, you do not have to do any follow up analyses – clearly the sex decision is quicker.

3. The test of the interaction between Prime and Task factors was also significant, F(2,36) = 13.87, p < .001. Therefore, the effect of the Prime factor is NOT the same for each level of the Task factor i.e. not the same for familiarity and sex decisions to the target faces. The graph below indicates that there is no real effect of the prime manipulation for sex decisions, but for familiarity decisions, the target faces are processed most quickly in the related condition, when compared to unrelated and neutral conditions. This time I got Excel to do a bar chart rather than a line chart. You could try this yourself, entering the individual cell means which were given above, and setting up appropriate labels etc.

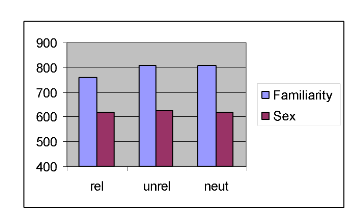
As well as helping us understand the statistically significant interaction between the two factors, the graph also makes clear that overall, Sex decisions are quicker than familiarity decisions (i.e. the graph certainly suggests a main effect of Task).

4. So, the results show that the main effect of the Prime factor is not the same for the two tasks, given that the interaction between the two factors is significant. Remember that once you have a significant interaction, this means that you cannot just interpret the results in terms of main effects. You need to really look at the individual cell means, not just any marginal means). Inspecting the graph gives us good idea of the nature of the interaction, as we saw in the answer to question 3.

In fact, it would be necessary to follow-up the statistically significant interaction, carrying out simple effect analysis (see later lecture), to check if there is a significant effect of the Prime factor only for familiarity decisions, and not for the Sex decisions. You could do this by doing a one factor repeated measures ANOVA (see Lecture 2) for the familiarity data (coded 1) and then the same thing for the sex decision data (coded 2). One way to do this would be to go to Data in SPSS, then Split File, and ask to “organise the output by groups”, using the groups based on the Task factor. Then just run the one factor repeated measures ANOVA, and it will give you the results separately for each group.

Dig deeper into Parent-Child Interaction Therapy with our selection of articles.